- Введение
- Глава 1. Переправа, переправа. Берег левый, берег правый
- Глава 2. Сообрази и посчитай
- Глава 3. Волшебное зеркало мага
- Глава 4. Где же правда?
- Глава 5. Установим соответствие между элементами различных множеств - решим задачу
- Глава 6. Упорядочим множество - решим задачу
- Глава 8. Определите победителя турнира
- Глава 9. Числовые ребусы
- Решения задач
- Ответы
Введение
Необычность этой книги состоит в том, что она предназначена для учащихся начальной школы.
Конечно, разница в уровне подготовки учеников различных классов начальной школы велика, и поэтому автор делает попытку сориентировать учащихся и преподавателей в степени трудности предлагаемых задач. С этой целью задачи, доступные школьникам первого класса, помечены одной звездочкой, второго — двумя, третьего — тремя звездочками.
Однако эта ориентация весьма условна. Возможность решения логической задачи в значительной степени зависит как от способностей ученика, так и от заинтересованности в том учителя.
В связи с этим мы надеемся, что использование преподавателями начальных классов материала, изложенного в предлагаемой книге, будет постепенно усложняться от класса к классу, и это позволит усилить логическую подготовку учащихся.
Отметим, что задачи различных разделов книги не связаны между собой и поэтому могут решаться в любом порядке.
Среди математических задач особое место занимают логические.
Отметим их важные особенности.
Во-первых, логические задачи отличаются от большинства математических тем, что для их решения, как правило, не требуется большого запаса математических знаний и можно ограничиться только некоторыми сведениями из арифметики.
Во-вторых, логические задачи почти всегда носят занимательный характер и этим привлекают даже тех, кто не любит математики. И, главное, их решение развивает логическое мышление, что способствует не только лучшему усвоению математики, но и успешному изучению основ любой другой науки.
Можно выделить несколько классов логических задач, решение которых сводится к использованию определенных приемов. В связи с этим в предлагаемой книге выделены следующие разделы:
- Переправа, переправа. Берег левый, берег правый. (Задачи о переправах.)
- Сообрази и посчитай. (Задачи, требующие небольших логических рассуждений с последующим арифметическим просчетом.)
- Волшебное зеркало мага. (Обобщение известной задачи о колпаках.)
- Где же правда? (Задачи о лгунах.)
- Установим соответствие между элементами различных множеств — решим задачу. (Решение логических задач с помощью таблиц и графиков.)
- Упорядочим множество — решим задачу.
- Можно ли обыграть противника, а если можно, то как это сделать? (Игровые логические задачи.)
- Определите победителя турнира. (Турнирные задачи.)
- Числовые ребусы.
Задачи каждого раздела анализируются и для них указываются способы решения, которые иллюстрируются примерами.
При этом в каждом разделе дается по несколько задач, предназначенных для самостоятельного решения.
В конце книги даны полные решения каждой из приведенных задач. Однако мы надеемся, что читатель будет обращаться к ним или в случае, когда задача им решена, или после многократных, но безуспешных попыток самостоятельно ее решить.
Как уже указывалось, для лучшей ориентации в степени сложности задачи помечены звездочками и кроме того пронумерованы двумя цифрами. Первая цифра указывает номер раздела, а вторая — номер задачи в разделе.
Многие из задач, включенных в книгу, заимствованы из различных источников. Так как книга предназначена для учащихся начальных классов, то большая часть их была предварительно адаптирована.
Глава 1. Переправа, переправа. Берег левый, берег правый
Ряд логических задач предусматривает переправу через реку с одного берега на другой. При этом обычно трудности переправы связаны с недостатком плавательных средств (одна лодка) и с количеством и особенностями пассажиров.
Рассмотрим несколько таких задач.
* Задача № 1.1. Десять солдат подошло к левому берегу реки, и им всем нужно переправиться на другой берег. У берега в челноке плавали два подростка. Других плавательных средств не было. Челнок может выдержать на воде двух подростков или одного взрослого человека.
Как организовать переправу солдат на правый берег, и за сколько рейсов это можно сделать?
Решение задачи № 1.1. Посчитаем количество рейсов с берега на берег для переправы одного солдата.
Первый рейс. Подростки вдвоем на челноке переправляются на правый берег.
Один из подростков остается на правом берегу, а второй подросток на челноке возвращается на левый берег.
Второй рейс. На левом берегу подросток покидает челн, передав его одному из солдат. Солдат переправляется на правый берег и передает челн второму подростку.
Второй подросток переправляется на левый берег. Таким образом, для переправы одного солдата потребовалось два рейса. Значит, для переправы десяти солдат потребуется двадцать рейсов.
* Задача № 1.2. Как перевезти в лодке с одного берега на другой волка, козла и капусту, если известно, что волка нельзя оставить без присмотра с козлом, а козел «неравнодушен» к капусте. В лодке только два места, поэтому можно брать с собой одновременно или одно животное, или капусту.
Решение задачи № 1.2. Опишем организацию перевозки с левого берега на правый волка, козла и капусты, при которой без присмотра не будут оставаться одновременно волк с козлом или козел с капустой.
В первом рейсе перевозчик берет с собой козла, оставляя на левом берегу волка и капусту.
Переехав на правый берег, перевозчик оставляет там козла и возвращается на левый берег.
Во втором рейсе перевозчик берет с собой волка, оставляя на левом берегу капусту. Переехав на правый берег, перевозчик оставляет там волка, забирает с собой козла и возвращается с ним на левый берег.
В третьем рейсе перевозчик берет с собой капусту, оставляя на левом берегу козла. Переехав на правый берег, оставляет там капусту (с волком) и возвращается на левый берег.
И, наконец, в четвертом рейсе он перевозит с левого берега на правый козла.
* Задача № 1.3. Как перевезти в лодке с одного берега на другой козла, капусту, двух волков и собаку, если известно, что волка нельзя оставлять без присмотра с козлом и собакой, собака в «ссоре» с козлом, а козел «неравнодушен» к капусте? В лодке только три места, поэтому можно брать с собой не более двух животных или одно животное и капусту.
Глава 2. Сообрази и посчитай
Сюда отнесены логические задачи, в которых приходится найти цепочку логических рассуждений, позволяющих в итоге с помощью простых арифметических вычислений дать ответы на вопросы задачи.
** Задача № 2.1. Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым.
«Вот тебе меч-кладенец — говорит ему баба Яга. — Одним ударом ты можешь срубить либо одну голову, либо две головы, либо один хвост, либо два хвоста. Но запомни: срубишь один хвост — два вырастут, срубишь два хвоста — голова вырастет, срубишь голову — голова вырастет, срубишь две головы — ничего не вырастет».
За сколько ударов Иван-царевич может срубить Змею все головы и хвосты?
Решение задачи № 2.1. Так как, по условию задачи, только рубка двух голов Змея одновременно приводит к их полной ликвидации, то перед полной ликвидацией Змея необходимо добиться, чтобы у него оставалось только четное число голов. Поскольку Змей имеет три головы, то следует рубить ему хвосты так, чтобы это привело к получению еще трех голов. В связи с этим Иван-царевич может поступить следующим образом:
- Первыми тремя ударами Иван-царевич рубит каждый хвост пополам, и тогда у Змея будет шесть хвостов.
- Следующими тремя ударами Иван-царевич рубит хвосты Змея попарно и в результате получает к имеющимся трем хвостам еще три головы.
- Наконец, последними тремя ударами Иван-царевич рубит попарно шесть голов Змея, и тот побежден девятью ударами.
*** Задача N° 2.2. На соревнованиях по стрельбе Алеша десять раз выстрелил по стандартной мишени и выбил 76 очков.
Сколько было попаданий в «пятерку» и «семерку», если «девяток было четыре, а других попаданий и промахов не было?
** Задача № 2.3. У школьника была некоторая сумма денег монетами достоинством в 15 и 20 копеек. Причем двадцатикопеечных монет было больше, чем пятнадцатикопеечных.
Пятую часть всех денег школьник истратил, отдав две монеты за билет в кино. Половину оставшихся денег он отдал за обед, оплатив его тремя монетами.
Сколько монет каждого достоинства было у школьника в начале?
*** Задача № 2.4. Петя и Боря произвели по пять выстрелов в одну мишень, попав в «5» один раз, в «7» — два раза, в «8» — один раз, в «9» — два раза, в «10» — два раза, в «11» — один раз, в «12» — один раз.
Четырьмя последними выстрелами Петя выбил в 7 раз больше очков, чем первым.
Известно, что Петя и Боря оба попали в круг «10».
Кто из них попал в круг «12»?
*** Задача № 2.5. У двух братьев было стадо баранов. Они продали его и за каждого барана получили столько рублей, сколько голов было в стаде. Выручку стали делить пополам. Старшему брату — десятку, младшему — десятку и так несколько раз. Потом старший брат взял свою десятку, а младшему несколько рублей не хватило. Тогда старший вынул из кармана нож и отдал брату в компенсацию за недостающую сумму.
Спрашивается, сколько стоит нож?
Глава 3. Волшебное зеркало мага[1]
Эту историю рассказал в своих мемуарах досточтимый Бильбо Бэггинс. Вы, конечно, знаете, читатель, что Бильбо — знаменитый Взломщик, о котором рассказал Джон Рональд Руэл Толкин в увлекательной книге «Хоббит, или Туда и обратно», а также в некоторых следующих книгах, повествующих о борьбе великого мага Гэндальфа (он же Митрандир, или Серый странник) со злым волшебником Сауроном. В конце концов Гэндальф победил, завершив бессонными трудами освобождение древней страны гномов, эльфов и хоббитов. О, это захватывающие истории, полные необыкновенных приключений! Если бы Вы, дорогой читатель, слыхали хотя бы четверть того, что рассказал об этом Толкин, а Толкин говаривал, что знает лишь маленькую толику того, что рассказывают о Сером страннике, то Вы были бы подготовлены к любой, самой невероятной истории. Истории и приключения вырастали как грибы всюду, где бы он ни появлялся.
Впрочем, вернемся к хоббиту Бильбо Бэггинсу. Мы не будем здесь рассказывать потрясающую историю его приключений, но считаем своим долгом напомнить, что очень важная персона среди гномов — Торин Оукеншильд — сказал, что Бильбо его друг и собрат, а также «превосходный и дерзновенный хоббит, да не выпадет никогда шерсть на его ногах!» Может быть, Вы думаете, что этот гном мог такое сказать о любом хоббите с толстеньким брюшком? Ну уж нет! Никакая хоббичья нора (а наша история случилась как раз в хоббичьей, а значит, благоустроенной норе) со всеми припасами, заготовленными даже внуком Старого Тука, в котором, как известно, текла доля крови эльфов, не могла повлиять на неимоверно важного Торина.
Все дело в той беседе, которая состоялась перед походом за сокровищами гномов между Гэндальфом, Торином, его двенадцатью подданными — гномами и, конечно, при участии нашего Бильбо. Собственно говоря, это была не простая беседа, а настоящий урок волшебства, который дал гномам Гэндальф. И лучшим учеником оказался хоббит! Гэндальф знал заранее все способности хоббита, а Толкин описал волшебные приемы, которыми хоббит овладел. Но, видимо, оба попали под влияние гномов, которые, как известно, любят все прятать и все скрывать. Не зря поется в их таинственной песне:
И гномы, боясь наказанья с небес,
Уже не надеясь на силу чудес,
Укрылись в богатых подземных палатах —
И след их сокровищ навеки исчез.
Потому-то, наверное, Толкин и скрыл урок великого мага, благодаря которому Бильбо смог впоследствии отнять у мерзкого Голлума волшебное кольцо и благодаря которому Торин смог обучить множество молоденьких гномов в подземной Г имназии Г номов. Вот о чем поведал Бильбо в своих мемуарах о волшебном уроке мага.
…Итак, после хорошего ужина и десерта из кексов, кофе и доброго эля, Бильбо пригласил гостей посидеть у камина. Никто из них позже не смог вспомнить, с чего начался урок Гэндальфа. Кстати, Джон Толкин тоже этого не знает, но приводит в своих книгах многочисленные свидетельства того, как легко Серый странник читает мысли окружающих. Вероятно, и тогда Гэндальф удивил гномов этой своей способностью и пока по своему обыкновению тихонько покатывался со смеху, Бильбо удивленно спросил его, как он это делает. Во всяком случае, Бильбо начинает свой рассказ с того, каким неожиданно серьезным стал Гэндальф и как он пробурчал себе под нос: «…Ну что же, меня это развлечет, а вам будет полезно, а возможно, и выгодно, если вы хотите добраться до конца предстоящего приключения…»
— Прелестно! — сказал Гэндальф. — Уважаемый Торин! В каких капюшонах прибыли сюда гномы?
— В лучших отстежных капюшонах для хождения в гости, разумеется! Самых разных цветов: красного, белого, фиолетового, зеленого, серого, желтого… Лично у меня — голубой, с длинной серебряной кистью! Да, еще в нашем багаже есть запасные капюшоны, к вашим услугам, — ответил Торин с некоторым удивлением.
— Несите их все сюда! — распорядился Гэндальф.
Гномы Фили и Кили быстро принесли капюшоны. Целую кучу разноцветных капюшонов!
— К вашим услугам! — сказали Фили и Кили, вывалив эту кучу на стол и став рядком.
Гэндальф выбрал из кучи шесть красных, два синих и три белых капюшона, а все остальные велел спрятать. Затем он усадил в кружок пятерых гномов: Фили, Кили, Дори, Нори и Ори.
— Сейчас Бильбо погасит лампу, а я в темноте надену пять капюшонов пятерым гномам, — сказал волшебник. — Гаси, Бильбо!
Когда лампу через минуту зажгли, то все увидели, что на Фили был надет белый капюшон, на Кили — синий, на Дори, Нори и Ори — красные. Правда, Гэндальф тут же спросил пятерых гномов, видят ли они, какого цвета капюшоны на их головах, и выяснилось, что увидеть, какой капюшон у тебя на голове, невозможно.
— Ну и что дальше? — спросил Бильбо.
Вопрос прозвучал, возможно, недостаточно вежливо, ну как спросили бы вы, если бы в вашем доме орда гномов съела все припасы, а великий маг, который привел эту орду, затеял, на ночь глядя, непонятные игры с гномичьими капюшонами?
— А дальше я попрошу этих гномов назвать цвет капюшонов, которые на них надеты, — сказал маг. — И чтоб больше никто рот не открывал! Я думаю, что кто-то из них может решить эту задачу.
В полном молчании слышалось только обиженное сопение всех тринадцати гномов, которые, как известно, всегда сопят носом при значительном интеллектуальном напряжении. Прошло десять минут, но никто из пятерых не смог назвать цвета своего капюшона. Когда Гэндальф разрешил говорить, раздался общий возмущенный вопль гномов:
— Это нельзя сделать без зеркала! — кричали гномы.
— Вздор! — отрезал Гэндальф. — Вечно вам, гномам, нужны инструменты. Зеркала вам подай! Я утверждаю, что у каждого из вас уже есть замечательное волшебное зеркало. Да не озирайтесь, Ори, зеркало не на капюшоне, а под вашим крепким черепом! Думаю, что придется обратиться за помощью к хоббиту. Что вы думаете об этой задаче, Бильбо?
— Я хотел бы узнать у вас, милейший сэр, так ли важно для нас, что гномов именно пять, а капюшоны на них трех цветов? — спросил Бильбо, напуская на себя деловой вид (обычно предназначавшийся для тех, кто пытался занять у него денег).
— Внимание! Внимание! — воскликнул Гэндальф. — Хоббит задал себе правильный вопрос, хотя и несколько более общий, чем хотелось бы. Что бы вы хотели сказать, Бильбо?
— Я бы предпочел иметь поменьше всего этого: и гномов, и капюшонов — обиженно заявил хоббит, считавший, что вопрос он задавал вовсе не себе. — Уж гномов-то точно хватило бы двоих, а капюшонов тоже не больше, чем двух цветов, скажем, красные и синие.
— Хоббиты всегда хотят проблемы попроще, а припасов в кладовой — побольше, — прокомментировал Торин.
— Неплохо! — одобрил хоббита Гэндальф. — Вот вам два гнома — Балин и Двалин и три капюшона — два красных и один синий, дорогой Бильбо. Что будем делать?
— Н-ну… — протянул хоббит и глубоко задумался.
Через несколько минут он попросил погасить лампу, а когда ее зажгли, то на Балине был надет красный капюшон, а на Двалине — синий. Балин увидел на Двалине синий капюшон и сразу завопил:
— У Бильбо был один синий! Значит, на мне красный капюшон! Я понял, понял!
— Что бы ты понял, если на Двалине тоже был бы красный капюшон? — успокоил его Торин Оукеншильд. Балин замолчал.
— Вот это бы и понял, — солидно сказал Двалин. — Он бы тогда не орал как сумасшедший, а я бы знал, что на мне он не видит синего капюшона, то есть на мне красный!
— Что вы скажете, благороднейший? — спросил Гэндальф Торина. Торин принял величественный вид.
— Я думаю, что самый простой случай, когда гномов всего два и капюшонов два. Как говорят, третий лишний!
— Неплохое замечание — одобрил Гэндальф. Если бы я показал нашим пяти умникам — маг кивнул на задумчиво сидящую пятерку гномов в капюшонах трех цветов, — только пять капюшонов, то они уже давно все бы ответили на вопрос! Что-что, а арифметику гномы знают и отнимать для них не проблема.
Гномы снова обиделись, а Бильбо лукаво усмехнулся.
— Конечно, если бы вы, сэр, дали мне много капюшонов… Ну, скажем, даже по два обоих цветов, то задача бы имела решения! Так что не третий лишний, а четвертый, причем синий, глубокоуважаемый Торин!
— Да, — согласился Торин. — Три красных и один синий — не проблема, поэтому, дело не в количестве всех капюшонов, а в том, чтобы синий был только один…
— Еще лучше, если ни одного синего, — пробурчал Двалин.
— Конечно, — сварливо откликнулся Гэндальф, — тогда и думать не о чем! И почему это вы не любите задач? Задача с капюшонами трех цветов заведомо сложнее, чем двух, но даже для двух цветов эльф все сообразил бы в две секунды!
Это прозвучало не только совершенно невежливо по отношению к гномам, которые недолюбливали эльфов, ну и хоббита задело за живое. Опасаясь, что Торин опять примется за свои комментарии о проблемах попроще и припасах, Бильбо решил разобраться с капюшонами побыстрее.
— Я предлагаю, досточтимые гости, рассмотреть теперь трех гномов и взять сколько угодно красных капюшонов, — сказал он. — Мне кажется, я смогу объяснить, в чем здесь дело.
— А дело здесь в том, сколько с самого начала будет синих капюшонов, — сказал Ори, который уже добрых полчаса разглядывал синий капюшон, надетый на Кили. — Если бы синий капюшон был только один… Ори вздохнул. — Но их не может быть два!
— Да, если синих капюшонов будет три или больше, а красных тоже не меньше трех, то ни один гном не сможет сказать, какой на нем капюшон, — подтвердил Бильбо. — Нет, нет — поспешил он предупредить обиду гномов, которые сразу насупились, — никто не сможет! Если я вижу только два капюшона из трех, то третий (мой) может быть и красным, и синим, ведь и тех и других хватает на всех! А вот два или один синий и много красных — это два разных случая, которые необходимо обдумать. Даже не два, а три случая: когда будут надеты только красные капюшоны, когда на одном гноме будет синий и, наконец, когда на двух гномах будут два синих капюшона!
— Ну уж если синих будет два, то третий гном сразу догадается, что на нем красный капюшон! — заявил Торин. — Третьего-то синего нет.
— Верно! — обрадовался хоббит. — Осталось только два случая! Что же будет, если на Балине синий капюшон, на Двалине — красный и на мне тоже красный? Я вижу синий и красный, Двалин видит синий и красный, а Балин видит два красных. Балин уж точно не сможет ничего сказать (не обижайтесь, Балин, вы тут ни при чем!), а мы с Двалином можем подумать, что у нас синий капюшон…
— Лично я не знаю, — проворчал Двалин. — Может быть синий, а может быть красный…
— Нет, Двалин, если я представляю себе, что на мне синий капюшон, то тогда вы видите два синих — мой и Балина и, как сообразительный гном, сразу скажете, что ваш капюшон — красный!
Двалин вежливо поклонился, подтверждая, что хоббит не ошибается в оценке его несомненных достоинств.
— Если же вы молчите, — продолжал Бильбо, то тем самым даете мне знать, что на мне не синий, а красный капюшон!
— Отлично, — сказал Гэндальф, — любой из тех, на ком красный капюшон, в этом случае может назвать цвет своего капюшона. Остался только один случай, когда надеты три красных капюшона.
— Это уже просто! — заявил Бильбо. Главное сделано. Если в последующем случае я представлю себе, что на мне синий капюшон, то досточтимые гномы (поклон, к вашим услугам!) воспользуются нашими предыдущими рассуждениями и могут сказать, что на них надеты красные капюшоны.
Гномы удовлетворенно улыбнулись — хоббит явно относился к ним с надлежащим уважением и признавал полное равенство в способностях.
— Итак, — подытожил волшебник, — если все трое относятся друг к другу с уважением и могут представить себя на месте другого, то единственное условие успеха — чтобы синих капюшонов было хотя бы на один меньше, чем участников игры.
— Я считаю, что игра нечестная, — выступил Торин. — Что-нибудь сказать правильно могут только те, на ком красные капюшоны, которых, как все поняли, должно быть больше, чем количество гномов. А те, на ком капюшоны синие, ничего не говорят в любом из трех случаев!
— Вот что значит быть аристократом! — восхитился Гэндальф. — Права меньшинства у вас на первом месте, дорогой Торин Оукеншильд. Но здесь вы ошиблись. Те, кто не говорят, — говорят своим молчанием!
Пятеро гномов, которые все еще не могли определить цвета своих капюшонов, возбужденно зашевелились. Гэндальф любил парадоксальные фразы.
— Что же получается, на нас всех синие капюшоны? — спросил Ори. — Я же вижу, что это не так!
— Постойте! — вмешался Бильбо. — Сейчас мы разберемся и с вашим случаем и вы получите по кексу за ваше терпение. Но сначала мы должны закончить со случаем двух цветов. Мне еще не все ясно. Гномов в капюшонах двух цветов может быть сколько угодно — обозначим количество гномов буквой N. Пусть красных капюшонов будет R, а синих — В. Вы говорите по-английски, господа? R — red, В — blue. Итак, или R < N, или В < N — иначе все будут молчать, как аристократы! Еще одно условие, чтобы капюшонов хватило на всех: R + В >N, причем, если R + В = N , то задача решается вычислением, без лишних слов, как справедливо заметил высокочтимый Торин. Но здесь случаев бездна, если R + В > N , клянусь моим дедушкой Старым Туком!
— Стоит хоббиту ввести буквенные обозначения, как он уже пугается бездны, — насмешливо отметил Гэндальф. — У вас еще будет возможность спуститься на дно любой бездны. И вы убедитесь, что это дно существует!
— Хорошо, хорошо, — заторопился Бильбо, зная могущество Серого странника, которому не составит труда отправить нерадивого ученика в бездну, — сейчас все сделаем. Я полагаю, что есть один случай, когда все ясно. Пусть В < N и все В синих капюшонов надеты. Тогда те N — В гномов, на которых красные капюшоны, могут сразу сказать, что на них красные. А вот если надеты не все синие…
— Спускайтесь вниз! — подсказал волшебник.
— Так… если надето В – 1 синих капюшонов, — бормотал хоббит, — я сижу в красном, а думаю, что на мне синий…
Тогда снова кто-то из красных, например, Балин, скажет, что на нем. Он ведь будет видеть В синих! Значит, если эти, в красных капюшонах молчат, то на мне тоже красный капюшон! Понятно. А если надето В – 2 синих, и я их вижу, то предположив, что на мне синий капюшон, я могу утверждать, что теперь Балин, который сидит в красном капюшоне, может думать так, как я думал, когда видел В – 1 синих капюшонов. Немного посидим, помолчим, и Балин догадается, что на нем красный капюшон. О, так я действительно спускаюсь: В – 1, В – 2 … Неужели все случаи почти одинаковы до последнего, когда синих капюшонов не будет ни одного?
— Правильно. Теперь вы знаете секрет главного волшебства — Великое Зеркало, — сказал Гэндальф.
— Если число отложенных синих капюшонов равно 2, 1 или 0, то задача разрешима.
— А как же с тремя цветами? — закричали пятеро уставших гномов.
— Клянусь моим дедушкой, Старым Туком, — начал Бильбо, — теперь я знаю, что делать. Я думаю, что Дори, Нори и Ори могут определить цвет своих капюшонов! Скажи, Дори, на тебе может быть синий капюшон?
Дори подумал и ответил:
— Нет, не может, тогда Нори, Ори и Фили видели бы два синих капюшона (Кили, молчи!) и уже знали бы, что на них не синие капюшоны. Тогда они знали бы, что на них могут быть только красные и белые и могли бы не обращать внимание на двоих в синих капюшонах… Ой, но это же такой случай, который мы уже рассмотрели: три участника в капюшонах двух цветов! Они молчат, значит, на мне не синий капюшон!
— Великая Редукция! — провозгласил Гэндальф. Теперь вы знаете и второй секрет магов. Владельцы капюшонов двух цветов могут объединиться в одну группу «красно-белых», и задача сведется (редуцируется) к уже рассмотренной.
Гномы ликовали. Теперь они знали, как пользоваться волшебным зеркалом мага.
Их пыл несколько охладило предложение Гэндальфа каждому гному самостоятельно решить ряд более сложных задач.
Вот эти задачи:
** Задача № 3.1. Имеется 5 гномов. Им показали 3 красных и 4 синих капюшона. В темноте на них надели 3 красных и 2 синих капюшона, а остальные спрятали.
Кто из гномов может определить цвет надетого на него капюшона?
** Задача № 3.2. Имеется 5 гномов. Им показали 3 красных и 4 синих капюшона. В темноте на них надели 2 красных и 3 синих капюшона, а остальные спрятали.
Кто из гномов может определить цвета надетого на него капюшона?
*** Задача № 3.3. Имеется 3 гнома. Им показали 3 красных и 3 синих капюшона. В темноте на них надели 2 красных и 1 синий капюшон, а остальные спрятали.
Может ли кто-нибудь из гномов определить цвет надетого на него капюшона?
*** Задача № 3.4. Имеется 8 гномов. Им показаны 5 красных, 4 синих и 2 белых капюшона. В темноте на них надели 4 красных, 2 синих и 2 белых капюшона, а остальные спрятали.
Может ли кто-нибудь из гномов определить цвет надетого на него капюшона?
… Еще долго горели свечи в хоббичьей столовой и, если бы в этой благоустроенной норе были окна в столовой, то случайный прохожий мог бы с изумлением увидеть, как гномы и хоббит увлеченно надевают друг на друга разноцветные капюшоны, смотрят, молчат, а потом весело смеются и снова надевают! А великий волшебник глядит на всю компанию сквозь клубы и кольца дыма из своей трубки…
Глава 4. Где же правда?
(Задачи о лгунах)
Задачи такого типа определяются по принципу: имеется одно, два или три множества людей. Представители одного из множеств говорят только правду, представители другого — ложь, а представители третьего множества могут говорить как правду, так и ложь.
В задаче приводятся высказывания представителей указанных множеств. По этим высказываниям и некоторой дополнительной информации, данной в задаче, требуется установить истину.
Наиболее простым ее вариантом является тот, по условию которого имеется группа людей, и каждый ее представитель высказывает по два утверждения. При этом известно, что одно из них истинно, а другое — ложно.
При решении задач этого типа поступают так: берут одно из двух утверждений некоторого представителя этой группы людей и предполагают, что оно истинно.
Если при этом, рассматривая утверждения других членов группы, мы не приходим к противоречию, то делается вывод, что взятое нами исходное утверждение действительно истинно.
Если же при рассмотрении утверждений других членов группы мы приходим к противоречию, то делается вывод, что взятое нами за истинное утверждение одного из членов группы является ложным и, следовательно, второе его утверждение является истинным.
Рассмотрим пример такой задачи.
** Задача № 4.1. Три ученика различных школ города Новгорода приехали на отдых в один летний лагерь.
На вопрос вожатого, в каких школах Новгорода они учатся, каждый дал ответ:
Петя: «Я учусь в школе № 24, а Леня — в школе № 8».
Леня: «Я учусь в школе № 24, а Петя — в школе № 30».
Коля: «Я учусь в школе № 24, а Петя — в школе № 8».
Вожатый, удивленный противоречиями в ответах ребят, попросил их объяснить, где правда, а где ложь.
Тогда ребята признались, что в ответах каждого из них одно утверждение верно, а другое — ложно.
В какой школе учится каждый из мальчиков?
Решение задачи № 4.1. Предположим, что верно первое утверждение Пети: «Петя учится в школе № 24». Тогда, очевидно, будут ложными второе утверждение Пети и первые утверждения Лени и Коли. Но при этом истинными оказываются утверждения Лени и Коли: «Петя учится в школе № 30» и «Петя учится в школе № 8».
В результате исходного предположения мы пришли к противоречию: Петя оказался учеником трех школ. Значит, наше предположение об истинности первого утверждения неверно.
Предположим теперь, что верно второе утверждение Пети: «Леня учится в школе № 8». Тогда, очевидно, ложны первые утверждения Пети и Лени и второе утверждение Коли. Но при этом оказывается истинным второе утверждение Лени и первое утверждение Коли, которые не дают противоречия. Значит, Леня учится в школе № 8, Петя — в школе № 30, а Коля — в школе № 24.
Аналогично решается следующая задача:
** Задача № 4.2. Четыре спортсменки: Аня, Валя, Галя и Даша — заняли первые четыре места в соревновании по гимнастике, причем никакие две из них не делили между собой эти места. На вопрос, какое место заняла каждая из спортсменок, трое болельщиков ответили:
- Аня — второе место, а Даша — третье место.
- Аня — первое место, а Валя — второе место.
- Галя — второе место, а Даша — четвертое место.
Оказалось, что каждый из болельщиков ошибся один раз.
Какое место заняла каждая из спортсменок?
В формулировках более сложных задач не указывают, являются ли высказывания конкретного представителя группы истинными или ложными, а указывают лишь общее число истинных и ложных высказываний. При этом требуется установить, какие из высказываний являются истинными.
Чаще всего это удается сделать путем перебора предположений об истинности одной части высказываний и ложности остальных высказываний. Если предположения такого рода не приводят к противоречию, то мы приходим к решению задачи.
*** Задача № 4.3. Один из пяти братьев разбил окно.
Андрей сказал: «Это или Витя, или Толя».
Витя сказал: «Это сделал не я и не Юра».
Дима сказал: «Нет, один из них сказал правду, а другой неправду».
Юра сказал: «Нет, Дима, ты не прав».
Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду.
Кто разбил окно?
Задача № 4.4. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда врут. Путешественник, приехавший на остров, нанял жителя острова в проводники. Они пошли и увидели другого жителя острова. Путешественник послал проводника узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал, что туземец говорит, что он абориген.
Кем был проводник: пришельцем или аборигеном?
Задача № 4.5. На острове Трисельске имеется три деревни: Правдино, Чередово и Лгуново. Известно, что жители первой деревни всегда говорят только правду, жители третьей деревни только лгут, а жители второй деревни чередуют ложь с правдой. При этом первый ответ чередовцев может оказаться как правдой, так и ложью.
Как-то раз приезжий встретился с островитянами, которым он по характерным чертам дал следующие прозвища: Алощек, Косоглаз, Борода, Курнос и Длинноух. Желая узнать, в каких деревнях эти люди живут, приезжий попросил первых двух рассказать ему по порядку, кто из какой деревни родом.
Косоглаз ответил, что Борода — чередовец, Курнос — правдовец, Алощек также родом из Чередова, а Длинноух — лгуновец.
Борода, однако, утверждал, что Косоглаз — чередовец, Курнос из Лгунова, Алощек — правдовец, а Длинноух из Чередова.
Можно ли из полученных ответов сделать верные выводы о родной деревне каждого из пяти островитян?
Глава 5. Установим соответствие между элементами различных множеств — решим задачу
Множеством называется коллекция, собрание объектов, объединенных по некоторому признаку.
Можно говорить о множестве учеников в классе, о множестве рыб в пруду, о множестве яблок на яблоне и т.д.
Предметы, входящие в множество, называются его элементами.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств с одинаковым числом элементов, между элементами которых имеются некоторые зависимости и требуется установить эти зависимости.
Решению таких задач помогает использование различных таблиц и графиков. Для простаты рассмотрим сначала случай с одинаковым числом элементов. Здесь удобно пользоваться таблицей, состоящей из n × n клеток (n — число элементов в множестве). Данные задачи вносятся в соответствующие клетки таблицы, например, знаками + (положительный результат) или. (отрицательный), установленными путем логических рассуждений.
Если в рассматриваемой задаче каждому элементу первого множества должен соответствовать единственный элемент второго множества, а двум различным элементам первого множества соответствуют два различных элемента второго множества, то такое соответствие будем называть взаимно однозначным.
Ясно, что при таком соответствии между двумя множествами, заполняя таблицу, мы в каждой строке (столбце) должны получить только одну клетку со знаком +. Имея дело с таблицей n × n , будем в дальнейшем обозначать клетки таблицы буквами Lij, где i — номер столбца таблицы, a j — номер строки. Проиллюстрируем этот способ в ходе решения следующей задачи.
* Задача № 5.1. Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что один из нас блондин, другой — брюнет, третий — рыжий, но ни у кого цвет волос не соответствует фамилии».
Какой цвет волос у каждого из друзей?
Решение задачи № 5.1. Для решения задачи воспользуемся таблицей 3 × 3, отмечая по горизонталям фамилии, а по вертикалям — цвета волос беседующих.
| Фамилия | Цвета волос | ||
| Рыжие | Черные | Русые | |
| Белокуров | |||
| Чернов | |||
| Рыжов | |||
По условию задачи Белокуров — не блондин, Чернов — не брюнет, а Рыжов — не рыжий. Это позволяет поставить знак – в клетках L13, L22 и L31. Кроме того, по условию, Белокуров не брюнет и, значит, в клетке L21 также следует поставить знак – .
После этого таблица принимает следующий вид:
| Фамилия | Цвета волос | ||
| Рыжие | Черные | Русые | |
| Белокуров | – | – | |
| Чернов | – | ||
| Рыжов | – | ||
Так как между множеством фамилий участников беседы и множеством цветов их волос должно быть взаимно однозначное соответствие, то, очевидно, в клетках L11 и L23 следует поставить знак +. Но тогда в клетках L12 и L33 следует поставить знак – , а в оставшейся клетке L3I поставить знак +.
И таблица принимает следующий вид:
| Фамилия | Цвета волос | ||
| Рыжие | Черные | Русые | |
| Белокуров | + | – | – |
| Чернов | – | – | + |
| Рыжов | – | + | – |
Отсюда следует, что у Белокурова волосы рыжие, у Чернова — русые, а у Рыжова — черные.
При решении задач такого типа с помощью графиков поступают следующим образом: элементы множеств изображают точками плоскости. Если по условию задачи между двумя элементами этих множеств есть соответствие, то будем соединять такие элементы сплошной линией. Если же между двумя элементами множеств соответствия нет, то будем соединять их пунктирной линией.
Используя условие задачи, мы получим на графике наглядное изображение исходных данных, а далее путем логических рассуждений установим соответствие между остальными парами элементов этих множеств. Конечно, здесь при наличии взаимно однозначного соответствия каждый элемент одного из множеств будет соединяться сплошной линией только с одним элементом другого множества, а с остальными его элементами он будет соединяться пунктирными линиями.
Проиллюстрируем этот способ решения логических задач в ходе решения задачи № 5.1.
Будем изображать множество друзей и множество цветов их волос кругами, а элементы множеств — точками, помещенными в эти круги.
Так как по условию задачи у Чернова волосы не черные, у Белокурова — не русые, а у Рыжова — не рыжие, то соединим пунктирными линиями элементы множеств: «Чернов» и «черные», «Белокуров» и «русые», «Рыжов» и «рыжие». Кроме того, известно, что Белокуров не брюнет, то есть у него волосы не черные. Значит, элементы «Белокуров» и «черные» также нужно соединить пунктирной линией. В результате будет получен следующий график.
Теперь рассмотрим пример более сложной задачи. В ней, как и ранее, между элементами множеств имеется взаимно однозначное соответствие, но увеличено число элементов множеств.
** Задача № 5.2. Однажды в Артеке за круглым столом оказалось пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между томичем и Витей, санктпетербуржец — между Юрой и Толей, а напротив него сидели пермяк и Алеша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются.
Определите, в каком городе живет каждый из ребят.
Решение задачи № 5.2. Для решения задачи воспользуемся таблицей 5×5.
| Города | Имена | ||||
| Юра | Толя | Алеша | Коля | Витя | |
| Москва | |||||
| С.-Петербург | |||||
| Новгород | |||||
| Пермь | |||||
| Томск | |||||
Так как москвич сидит между томичем и Витей, то Витя не живет ни в Москве, ни в Томске. Это позволяет поставить знак — в клетках: L51 и L55.
Так как петербуржец сидел между Юрой и Толей, а напротив него сидели пермяк и Алеша, то Юра, Толя и Алеша не живут ни в Санкт-Петербурге, ни в Перми. Это позволяет поставить знак — в клетках: LI2, L14, L22, L24, L32, L34.
Так как Коля никогда не был в СанктПетербурге, Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются, то это означает, что Коля не живет в Санкт-Петербурге, Юра не живет ни в Москве, ни в Томске, а Толя не живет в Томске. Следовательно, знак — нужно поставить в клетках: L41, L11, L15, L25.
В результате таблица принимает вид:
| Города | Имена | ||||
| Юра | Толя | Алеша | Коля | Витя | |
| Москва | – | – | |||
| С.-Петербург | – | – | – | – | |
| Новгород | |||||
| Пермь | – | – | – | ||
| Томск | – | – | – | ||
Теперь, очевидно, нужно поставить знак + в клетках L51 и L13 и, следовательно, поставить знак – в клетках L53, L54, L23, L33, L43. Но тогда знак + нужно поставить в клетке L44 и знак – в клетках L41 и L45.
Теперь для полного заполнения таблицы остается поставить знак + в клетках L35 и L21, а – в клетке L31. И таблица принимает следующий вид:
| Города | Имена | ||||
| Юра | Толя | Алеша | Коля | Витя | |
| Москва | – | + | – | – | – |
| С.-Петербург | – | – | – | – | + |
| Новгород | + | – | – | – | – |
| Пермь | – | – | – | + | – |
| Томск | – | – | + | – | – |
Таким образом установлено, что Толя живет в Москве, Витя — в Санкт-Петербурге, Юра — в Новгороде, Коля — в Перми, а Алеша — в Томске.
Для решения этой задачи с помощью графиков следует рассмотреть два множества на плоскости (множество городов и множество мальчиков), в каждом из которых по пять элементов.
Используя условия задачи и правила соединения элементов множеств пунктирными и сплошными линиями, мы получим следующий график, дающий решение задачи.
Из рассмотренных примеров ясно, что с помощью графиков рационально решать задачи, в которых описываются множества с небольшим числом элементов.
Предлагаем решить следующую задачу двумя способами решения.
** Задача № 5.3. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что:
1) Вода и молоко не в бутылке.
2) Сосуд с лимонадом стоит между кувшином и сосудом с квасом.
3) В банке не лимонад и не вода.
4) Стакан стоит между банкой и сосудом с молоком.
В каком сосуде находится каждая из жидкостей?
Решение логической задачи усложняется, если в ней фигурирует не два, а большее число множеств. В этом случае или приходится пользоваться не одной, а несколькими таблицами, или изображать на плоскости больше двух множеств. Проиллюстрируем эту особенность на следующем примере.
Задача № 5.4. Три друга: Алеша, Боря и Володя — учатся в различных школах города Новгорода (в школах № 1, № 8 и № 30). Все они живут на различных улицах (улица Рогатица, улица Газон и улица Ломоносова). Причем один из них любит математику, второй — биологию, а третий — химию. Известно, что:
1) Алеша не живет на ул. Рогатица, а Борис не живет на ул. Газон.
2) Мальчик, живущий на ул.Рогатица, не учится в школе № 30.
3) Мальчик, живущий на ул. Газон, учится в школе № 1 и любит математику.
4) Володя учится в школе № 30.
5) Ученик школы № 8 не любит химию.
В какой школе учится каждый из друзей, на какой улице он живет и какой предмет любит?
Решение задачи № 5.4. Для решения этой задачи построим график. Видимо, здесь следует рассматривать на плоскости четыре множества: множество друзей, множество школ, множество улиц и множество школьных предметов, каждый из которых содержит три элемента.
Так как Алеша не живет на улице Рогатица, а Борис не живет на улице Газон, то пунктирными линиями следует соединить элементы множеств: «Алеша» — «улица Рогатица», «Боря» — «улица Газон».
Так как мальчик, живущий на улице Рогатица, не учится в школе № 30, то следует соединить пунктирной линией элементы множеств «улица Рогатица» — «школа № 30».
Так как мальчик, живущий на улице Газон, учится в школе N° 1 и любит математику, то сплошными линиями следует соединить элементы множеств: «школа № 1» — «математика», «школа № 1» — «улица Газон», «улица Газон» — «математика».
Так как Володя учится в школе № 30, то сплошной линией следует соединить элементы множеств «Володя» — «школа № 30».
Так как ученик школы № 8 не любит химию, то пунктирной линией следует соединить элементы множеств «школа № 8» — «химия».
Теперь видно, что ученик школы № 8 любит биологию, а ученик школы № 30 любит химию, и соответствующие элементы множеств нужно соединить сплошными линиями.
Как видно, ученик школы № 30 не живет на улицах Рогатица и Газон. Следовательно, он живет на улице Ломоносова, но тогда ученик школы № 8 живет на улице Рогатица и, значит, соответствующие элементы можно соединить сплошными линиями.
При этом, очевидно, соединяются сплошными линиями элементы множеств: «Рогатица» — «биология», «химия» — «Ломоносова», а график принимает вид:
Теперь ясно, что Алеша живет на улице Газон, учится в школе № 1 и любит математику, Боря живет на улице Рогатица, учится в школе № 8 и любит биологию и, наконец, Володя живет на улице Ломоносова, учится в школе № 30 и любит химию.
Аналогично задаче № 5.4 решается следующая задача.
Задача № 5.5. Три подруги вышли в белом, зеленом и синем платьях и туфлях. Известно, что только у Ани цвета платья и туфель совпадали. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях.
Определите цвет платья и туфель на каждой из подруг.
Значительно сложнее строятся рассуждения при решении логических задач, содержащих множества, между элементами которых нет взаимно однозначного соответствия. Здесь необходимо учитывать, что одному элементу первого множества может соответствовать два или более элементов второго множества и, следовательно, в строке или в столбце приходится ставить не один, а два или более знаков +.
Приведем пример такой задачи.
*** Задача № 5.6. На международном конгрессе встретились четверо ученых: физик, историк, биолог и математик. Национальности их были различными и, хотя каждый из ученых владел двумя языками из четырех (русский, английский, французский и итальянский), не было такого языка, на котором они могли бы разговаривать вчетвером. Был язык, на котором могли разговаривать сразу трое. Никто из ученых не владел французским и русским одновременно. Хотя физик не говорил по-английски, он мог быть переводчиком, если биолог и историк хотят поговорить друг с другом. Историк говорит по-французски и может говорить с математиком, хотя тот не знает ни одного русского слова. Физик, биолог и математик не могут беседовать втроем на одном языке.
Какими двумя языками владеет каждый из ученых?
Решение задачи № 5.6. Для решения задачи воспользуемся таблицей 4×4:
| Языки | Профессия | |||
| Физик | Историк | Биолог | Математик | |
| Русский | ||||
| Английский | ||||
| Францухкий | ||||
| Итальянский | ||||
Учтем, что между множеством ученых и множеством языков взаимно однозначного соответствия нет, и каждому элементу из множеств ученых соответствуют два элемента из множества языков, то есть в каждом столбце таблицы должно быть по два знака + и по два знака –.
Запишем в таблицу данные, которые непосредственно вытекают из условия задачи: физик не говорит по-английски, историк говорит порусски (и, значит, не говорит по-французски), математик не знает русского языка. Эти данные позволяют поставить знак + в клетке L21, и знак – в клетках L12, L23, L41. Также знак — можно поставить в клетке L31, так как биолог не может говорить с историком без переводчика и, следовательно, он не знает русского языка.
Установим язык, на котором могли разговаривать сразу трое ученых. Это не может быть русский язык, так как русским языком не владеют биолог и математик. Это не может быть английский язык, так как им не владеет физик, и если бы им владели одновременно историк, биолог и математик, то историк и биолог обходились бы при разговоре без переводчика.
Если теперь предположить, что таким языком является французский, то на нем должны говорить физик, биолог и математик. Но по условию задачи они не могут беседовать на одном языке втроем. Следовательно, языком, на котором могли разговаривать сразу трое ученых, является итальянский, и говорят на нем физик, историк и математик.
Действительно, физик, биолог и математик не говорят на одном языке, а историк и биолог не обходятся без переводчика. Поставим знак + в клетках L14, L24, L44.
Теперь из таблицы видно, что историк не владеет английским языком. При этом ясно, что физик может быть переводчиком в разговоре историка с биологом только в случае, если биолог и физик владеют французским языком (биолог не знает русского и итальянского, а физик не знает английского). Но если физик знает французский язык, то он не владеет русским.
И, наконец, математик не знает французского языка, так как в противном случае физик, биолог и математик говорили бы на одном языке. Поэтому математик владеет английским языком. В связи со сказанным нужно поставить знак + в клетках L13, L32, L42 и знак – в оставшиеся клетки.
| Языки | Профессия | |||
| Физик | Историк | Биолог | Математик | |
| Русский | – | + | – | – |
| Английский | – | – | + | + |
| Францухкий | + | – | + | – |
| Итальянский | + | + | – | + |
Следовательно, физик владеет французским и итальянским языками, историк — русским и итальянским, биолог — английским и французским, математик — английским и итальянским.
Глава 6. Упорядочим множество — решим задачу
Слово «порядок» часто употребляется и в обыденной речи, и в математике. Мы говорим о порядке слов в предложении, о порядке выполнения действий при решении задачи, о порядке номера дома на некой улице.
При этом в слово «порядок» включают такой смысл: оно означает, какой элемент того или иного множества за каким следует (или какой элемент какому предшествует).
Если для элементов некоторого множества М установлен порядок его элементов, то говорят, что множество М упорядочено.
Ясно, что если множество М состоит из конечного числа элементов и упорядочено, то все его элементы можно занумеровать и изобразить точками прямой, расположенными в определенном порядке. Далее мы будем говорить и об упорядоченных парах элементов двух множеств.
Рассмотрим класс логических задач, в которых решение сводится к упорядочению некоторых множеств.
Задача № 6.1. В очереди за билетами в кино стоят: Юра, Миша, Володя, Саша и Олег. Известно, что:
1) Юра купит билет раньше, чем Миша, но позже Олега.
2) Володя и Олег не стояли рядом.
3) Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей.
Кто за кем стоит?
Решение задачи № 6.1. По условию задачи в очереди за билетами три мальчика стоят в порядке: Олег, Юра и Миша.
Поэтому нужно установить места в очереди для Саши и Володи.
Но Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Это возможно лишь в случае, когда Саша стоит за Мишей, а остальные мальчики стоят перед Мишей.
Теперь нужно установить место Володи в очереди. По условию задачи Володя не стоит рядом ни с Олегом, ни с Сашей. Значит, Володя стоит между Юрой и Мишей.
Таким образом, мальчики стоят в очереди в следующем порядке: Олег, Юра, Володя, Миша и Саша.
Задача № 6.2. Волейбольные команды: А, Б, В, Г, Д и Е — разыграли первенство. Известно, что команда А отстала от Б на три места, команда В оказалась между Г и Д, команда Е опередила Б, но отстала от Д.
Какое место заняла каждая из команд?
** Задача № 6.3. В семье четверо детей. Им 5, 8, 13 и 15 лет. Детей зовут Аня, Боря, Вера и Галя.
Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на три?
Следующая задача является простейшим примером упорядочения пар двух множеств.
* Задача № 6.4. Четыре подруги пришли на каток, каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре «кавалер» выше «дамы», и никто не катается со своей сестрой. Самый высокий из компании — Юра Воробьев, следующий по росту — Андрей Егоров, потом Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Инна Крымова и Аня Воробьева.
Кто с кем катался?
*** Задача № 6.5. На улице, встав в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя.
1) Девочка в зеленом платье — не Аня и не Валя — стоит между девочкой в голубом платье и Надей.
2) Девочка, в белом платье стоит между девочкой в розовом платье и Валей.
Какого цвета платье у каждой из девочек?
Следующая задача также приводит к необходимости упорядочить пары элементов двух множеств. Это упорядочение имеет особый характер.
*** Задача № 6.6. Как-то раз четыре товарища (Петя, Боря, Алеша и Коля) пошли со своими сестрами на школьный новогодний бал.
Во время первого танца каждый из них танцевал не со своей сестрой. Лена танцевала с Петей, а Светлана — с братом Наташи, Оля танцевала с братом Светланы, Боря — с сестрой Алеши, а Алеша — с сестрой Пети.
Кто чей брат и кто с кем танцевал?
Будем изображать в виде прямоугольников места расположения участников новогоднего бала с учетом условий задачи. Тогда получим, очевидно, четыре прямоугольника следующего вида:
Пользуясь условиями задачи и логическим обоснованием отдельных положений, будем заполнять пустые места в прямоугольниках следующим образом:
Петя — не брат Лены (Лена танцевала не со своим братом), не брат Наташи (Светлана танцевала с братом Наташи), не брат Светланы (Оля танцевала с братом Светланы). Значит, Петя — брат Оли, а Оля сестра Пети. Это помечается в прямоугольниках 1 и 3.
Так как Алеша танцевал с сестрой Пети, то он танцевал с Олей (пометка в прямоугольнике 3). Но Оля танцевала с братом Светланы. Значит, Алеша — брат Светланы (пометка в прямоугольниках 2 и 3). Но Боря танцевал не с сестрой Алеши. Значит, Боря танцевал со Светланой. Но Светлана танцевала с братом Наташи. Значит, Боря — брат Наташи. Теперь ясно, что Лена — сестра Коли, а Коля танцевал с Наташей.
*** Задача № 6.7. Алексей Иванович, Федор Семенович, Валентин Петрович и Григорий Аркадьевич были как-то со своими детьми в парке культуры и отдыха. Они катались на колесе обозрения. В кабинах колеса оказались вместе: Леня с Алексеем Ивановичем, Андрей с отцом Коли, Тима с отцом Андрея, Федор Семенович с сыном Валентина Петровича, а Валентин Петрович с сыном Алексея Ивановича.
Назовите, кто чей сын и кто с кем катался, если ни один из мальчиков не катался со своим отцом.
Задача № 6.8. Жили четыре друга. Звали их Альберт, Карл, Дидрих и Отто. Фамилии друзей те же, что имена, однако ни у кого из них имя и фамилия не были одинаковы. Кроме того, фамилия Дидриха не была Альберт.
Требуется определить фамилию каждого из друзей, если известно, что имя мальчика, чья фамилия Отто, есть фамилия того мальчика, имя которого — фамилия Карла.
Решение задачи № 6.8. Будем обозначать имя и фамилию каждого мальчика двумя буквами в виде XY, где X — первая буква имени, a Y — первая буква фамилии.
Из условия задачи следует, что нет мальчиков, соответствующих символам АA, ДD, КK, OO, ДА. Но есть мальчик XY такой, что ему соответствуют мальчики YO и КK. Рассмотрим возможные значения букв X и Y для трех мальчиков.
Ясно, что X не К (иначе было бы два мальчика с именем Карл), X не О (иначе было бы два мальчика с фамилией Отто).
Аналогично, X не К и не О.
Следовательно, X и Y могут принимать только значения А и Д. Но по условию задачи нет мальчика, соответствующего символу ДA. Значит, возможен лишь единственный вариант: Х = А, Y = Д.
Таким образом, мальчики с именами Альберт, Карл, Дидрих и Отто имеют фамилии соответственно: Дидрих, Альберт, Отто и Карл.
Задача № 6.9. (Любовь без взаимности).
Трое юношей: Коля, Петя и Юра — влюблены в трех девушек: Таню, Зину и Галю. Но это любовь без взаимности.
- Коля любит девушку, влюбленную в юношу, который любит Таню.
- Петя любит девушку, влюбленную в юношу, который любит Зину.
- Зина не любит Юру.
Кто в кого влюблен?
Глава 7. Можно ли обыграть противника? А если можно,
то как это сделать?
(Игровые логические задачи)
Игровые логические задачи широко распространены в литературе по занимательной математике.
Для учащихся младших классов наиболее интересны и доступны задачи-игры, в которых участвует два игрока. Будем в дальнейшем называть участников таких игр «начинающим» и «противником».
В предлагаемых играх требуется установить наличие выигрышной стратегии для начинающего или противника, а в случае ее отсутствия показать, что при правильной игре участников она может закончиться только ничейным результатом.
Рассмотрим простую задачу такого типа.
Задача № 7.1. Имеется кучка камней. Двое играющих (начинающий и противник) по очереди берут по своему усмотрению один, два или три камня. Проигрывает тот, кто возьмет последний камень.
а) В кучке шесть камней.
Как должен играть начинающий, чтобы выиграть? Как должен играть противник, если начинающий в одном из своих ходов допустил ошибку? Как меняется план игры, если в кучке семь или восемь камней?
б) В кучке одиннадцать камней.
Как должен играть начинающий, чтобы выиграть? Как должен играть противник, если начинающий в одном из своих ходов допустил ошибку?
Решение задачи № 7.1.
а) Пусть в кучке шесть камней. Расположим их в ряд, выделив первый и последний камни, а в середине — группу из четырех камней.
Рассмотрим различные варианты игры в поисках стратегии игры начинающего, при которой он выигрывает. Эта стратегия должна обеспечить такой порядок ходов начинающего, при котором к последнему ходу противника остается не взятым только один камень.
Так как начинающий своим первым ходом может взять один, два или три камня, то возможно три варианта:
- Первым ходом начинающий берет три камня. Тогда противник, взяв два камня, выигрывает, так как начинающему остается один камень.
- Первым ходом начинающий берет два камня. Тогда противник, взяв три камня, выигрывает, так как начинающему остается опять один камень.
- Начинающий берет один камень. Тогда при любом числе камней, взятых противником из четверки камней, начинающему останется из этой четверки один, два или три камня, которые он может забрать своим вторым ходом, оставляя противнику один последний камень. Значит, выигрывает начинающий.
Пункт 3 дает выигрышную стратегию игры начинающего. В пунктах 1 и 2 рассматриваются ситуации, при которых начинающий совершает ошибку при своем первом ходе, и там же указывается выигрышная стратегия противника при этой ошибке начинающего. Но начинающий может допустить ошибку при своем втором ходе. Действительно, пусть после первого хода начинающего противник взял один камень, а начинающий своим вторым ходом взял один или два камня (или противник взял два камня, а начинающий своим вторым ходом взял один камень). Тогда противниц получает возможность взять оставшиеся от четверки камни и тем самым встать в позицию начинающего, то есть оставить начинающему последний камень.
Пусть теперь в кучке семь или восемь камней. Тогда их можно расположить следующим образом:
При этом ясно, что начинающему для получения выигрышной стратегии необходимо изменить только свой первый ход (в случае семи камней брать при первом ходе два, а в случае восьми — брать при первом ходе три камня).
б) Допустим, в кучке одиннадцать камней. Расположим их в ряд, выделив два первых и последний камень, а между ними две группы по четыре камня.
Для получения выигрышной стратегии начинающему, очевидно, нужно своим первым ходом взять два камня, а после каждого хода противника брать столько, чтобы сумма камней, взятых этим ходом начинающего и предыдущим ходом противника, равнялась четырем.
Как вести себя противнику, если начинающий в одном из своих ходов допустил ошибку?
Если начинающий своим первым ходом взял не два, а один камень, то противнику следует взять также один камень, и он становится в позицию начинающего, а поэтому выигрывает.
Если начинающий своим первым ходом взял не два, а три камня, то противнику следует взять также три камня, и он становится в позицию начинающего, а поэтому выигрывает.
Наконец, если начинающий допустил ошибку во втором ходе, например, противник взял из первой четверки камней один, а начинающий — один или два камня, то противнику следует взять последние камни этой четверки, и тогда он выигрывает.
Задача № 7.2. Двое заняты такой игрой: имеется четырнадцать камней; играющие берут по своему усмотрению один, два или три камня, по очереди. Выигрывает тот, кто берет последний камень.
Как должен играть начинающий, чтобы выиграть? Как должен играть противник, если начинающий в одном из своих ходов допустил ошибку?
Характер игры несколько меняется, если в ее условиях рассматривается две кучки камней.
Ниже приводится простейшая игра такого типа.
* Задача № 7.3. Имеется две кучки камней. Игра состоит в том, что каждый из двух играющих по очереди берет произвольное количество камней из любой, но одной кучки. Выигрывает тот, кто возьмет последний камень.
- Кто выиграет (начинающий или противник), если в первой кучке 30 камней, а во второй — 16 ?
- Кто выиграет, если в каждой кучке по 15 камней?
Следующие две задачи по своим формулировкам отличаются от задачи № 7.3, но основные идеи в их решении те же.
* Задача № 7.4. На самом левом поле клетчатой полосы 1×10 лежат две пуговицы. Двое играют в следующую игру: каждый из них может перенести любую пуговицу (но только за один ход) вправо на любое число полей, вплоть до последнего поля. Проигрывает тот, кому некуда ходить.
Докажите, что при правильной игре противника начинающий всегда проигрывает.
Задача № 7.5. На самом левом поле клетчатой полосы 1×10 лежат три пуговицы. Двое играют в следующую игру: каждый может переместить любую пуговицу (но только за один ход) вправо на любое число полей. Проигрывает тот, кому некуда ходить.
Докажите, что начинающий игру может обеспечить себе победу. Проанализируйте стратегию противника для выигрыша, если начинающий не знает выигрышной стратегии.
Среди учащихся младших классов широко распространена игра в «крестики-нолики» на доске 3×3. Как известно, при правильной игре начинающего и противника игра в «крестики-нолики» приводит только к ничейному результату.
Приведем еще одну игру в «крестики-нолики», но по измененным правилам.
* Задача № 7.6. Двое играют в «крестики-нолики» на доске 3×3 по измененным правилам. Каждый при своем ходе может поставить как «крестик», так и «нолик». Выигрывает тот, после хода которого образуется три подряд стоящих одинаковых значка (по вертикали, горизонтали или диагонали как в обычных «крестиках-ноликах»).
Кто выиграет — начинающий или противник? И как?
** Задача № 7.7. Двое мальчиков играют: они по очереди ставят ладьи на шахматную доску. Выигрывает тот, после последнего хода которого все клетки оказываются побитыми поставленными фигурами.
Кто победит, если оба стараются играть наилучшим образом?
Задача № 7.8. Играют двое. Первый участник называет произвольное целое положительное число, не превышающее четырех, то есть он может назвать числа: один, два, три, четыре. Второй игрок прибавляет к названному свое целое число, также не превышающее четырех, и называет сумму. К этой сумме первый прибавляет какое-либо положительное число, не превышающее четырех, и сообщает сумму. Выигрывает тот, кто первым достигает числа 26.
Решение задачи № 7.8. Выигрышную стратегию имеет начинающий. Действительно, если он первым называет число 1, а в дальнейшем, после того как противник назовет число k1, (не больше четырех), называет число (5–k,) (i = l, 2, 3, 4, 5), тогда в итоге будет называться сумма:
1 + k1 + (5 – к1) + k2 + (5 – k2) + k3 +
+ (5 – k3) + k4+ (5 – k4) + k5 + (5 – k5) =
= 1 + (k1 + k2 + k3 + k4 + k5) –
– (k1 + k2 + k3 + k4 + k5) + 5×5 = 26,
причем числа 26 достигает начинающий, так как он последний назовет число 5 – k5, добавление которого к предыдущей сумме и даст число 26.
Задача № 7.9. Играют двое. Первый участник игры называет произвольное целое положительное число, не превышающее десяти, то есть он может назвать число десять и всякое меньшее десяти положительно число. Второй игрок прибавляет к названному числу свое целое положительное число, также не превышающее десяти, и называет сумму. К этой сумме первый прибавляет какое-либо положительное число, не превышающее десяти, и сообщает сумму. Выигрывает тот, кто первый достигает ста.
Как добиться победы?
Глава 8. Определите победителя турнира
(Турнирные задачи)
Здесь рассматривается класс логических задач, связанных с выяснением итогов некоторых турниров. В задачах этого класса обычно приводятся неполные данные об итогах проведенных спортивных встреч и требуется путем логических рассуждений получить полные данные.
Естественно, что в большинстве случаев решению задачи способствует оформление турнирной таблицы по данным, приведенным в условиях задачи, а затем по данным, полученным логическим путем. Конечно, решая задачу о шахматном или футбольном турнире, нужно знать основные положения о таких турнирах.
Так в шахматном турнире победитель игры в партии получает одно очко, ничейный исход оценивается для каждого игрока в 0,5 очка, а проигравшему записывается нуль очков.
В шахматном турнире участники, набравшие одинаковое количество очков, делят между собой соответствующие места.
Если в шахматном турнире участвует n шахматистов, то турнирная таблица представляет собой таблицу, содержащую n×п клеток. Как пример, изобразим таблицу шахматного турнира, в котором участвует пять шахматистов и первые буквы их фамилий: А, Б, В, Г, Д.
В этом случае турнирная таблица имеет вид:
Диагональные клетки таблицы заштриховываются, так как ни один участник турнира не играет сам с собой, и поэтому в диагональных клетках результаты встреч не отмечаются.
При фиксировании результата встречи, например, между участниками Б и Г при выигрыше Б в клетке на пересечении строки Б и столбца Г ставится 1, а в клетке на пересечении строки Г и столбца Б ставится 0 (как показано в таблице).
В случае ничейного исхода встречи в указанных клетках записывается по 0,5.
Количество очков в каждой строке таблицы суммируется, и места в итоге турнира распределяются в соответствии с набранным количеством очков.
В футбольном (хоккейном) турнире команда-победитель получает два очка. Ничейный исход оценивается для каждой команды в одно очко, а поражение — в нуль очков.
При распределении мест в футбольном (хоккейном) турнире в случае равенства очков у двух команд во внимание принимается разница забитых и пропущенных голов.
От шахматной турнирной таблицы незначительно отличается футбольная (хоккейная) таблица. Так, для футбольного турнира, в котором участвует четыре команды: «Зенит», «Спартак», «Динамо», «Авангард» — таблица будет иметь вид:
В отличие от шахматной таблицы здесь часто результат встреч записывается в соответствующих клетках как соотношение забитых и пропущенных мячей. Конечно, в отдельных случаях могут проставляться и очки.
Так, если команда «Зенит» выиграла у команды «Динамо» со счетом 3:1, то в клетке на пересечении строки «Зенит» и столбца «Динамо» записывается счет 3:1 (смотри таблицу), а в клетке на пересечении строки «Динамо» и столбца «Зенит» записывается счет 1:3 (или соответственно 2 и 0).
Задача № 8.1. Шесть шахматистов: А, Б, В, Г, Д, Е сыграли в турнире между собой по одной партии. А сыграл все партии вничью. Б не выиграл ни одной партии. В выиграл у победителя соревнования и сыграл вничью с Д. Г обогнал Д, но отстал от Е.
Кто сколько очков набрал и какое место занял?
Решение задачи № 8.1. Для удобства решения задачи будем заполнять турнирную таблицу, используя данные задачи, сформулированные в явном виде: во всех клетках, связанных с А, нужно поставить по 0,5 очка и отметить ничью в игре между Б и Д.
Установим победителя турнира. Это не А (по количеству очков), не Б (он не выиграл ни одной партии), не В (он выиграл у победителя), не Г (он отстал от Е), и не Д (его обогнал Г). Следовательно, победителем является Е. И он по условию задачи проиграл В. Значит, в последней клетке горизонтали В нужно поставить 1, а в третьей клетке горизонтали Е поставить 0.
Как сыграли Е и Б? Б не выиграл у Е (иначе у Е было бы 2,5 очка, и он не мог бы стать победителем). Но по условию задачи Б не проиграл Е. Значит, они сыграли вничью, и поэтому в соответствующие клетки нужно поставить по 0,5.
Чтобы Е был победителем, он должен набрать не менее трех очков, то есть больше, чем набрал А. Но тогда Е выиграл у Г и Д, и поэтому в горизонтали Е в четвертой и пятой клетках следует поставить 1, а в шестой клетке горизонталей Г и Д — 0.
По условию задачи Б не проиграл ни одной партии. Но тогда у него не меньше 2,5 очков. У него не может быть больше 2,5 очков, иначе он догонит победителя. Значит, у Б 2,5 очка, а это значит, что он все партии сыграл вничью. Таким образом, во всех клетках горизонтали и вертикали Б должно стоять 0,5.
Теперь ясно, что В проиграл Г, в противном случае у него будет больше, чем 2,5 очка.
Так как Г обогнал Д, то Д не мог выиграть у Г, иначе у Д будет 2,5 очка, а у Г — 2 очка. Но и Г не мог выиграть у Д, иначе он догоняет победителя. Значит, Г и Д сыграли вничью.
Внося теперь в таблицу данные и о выигрыше В и Г, и о ничейном результате между Г и Д, мы получим ответы на все вопросы, поставленные в задаче.
*** Задача № 8.2. В финальном турнире играли пять шахматистов. А окончил все партии вничью. Б сыграл вничью с занявшим первое и последнее место. В проиграл Б, но зато сыграл вничью только одну партию. Г выиграл у Д и у занявшего четвертое место. Д не выиграл ни одной партии.
Кто сколько очков набрал и какое место занял?
*** Задача № 8.3. Недавно я нашел прошлогоднюю таблицу хоккейного турнира между шестыми классами нашей школы. На ней сохранилась лишь небольшая часть записей:
Попробуйте восстановить таблицу.
Решение задачи № 8.3. Команда 6в класса, занявшая первое место, набрала 5 очков. Действительно, из 12 очков, которые разыгрывались в турнире, 4 очка набрали в сумме команды классов 6г и 6б. Следовательно, команды классов 6а и 6в в сумме набрали 8 очков. Команда класса 6в не могла набрать меньше 5 очков, так как в противном случае (при 4 очках) команда 6а класса также имела бы 4 очка и лучшее, чем у команды 6а класса соотношение забитых и пропущенных голов (6:3). Значит, на первом месте была бы команда 6а класса. Но команда 6в класса не могла набрать и 6 очков, так как для этого нужно было иметь три победы, а общий счет 3:1, указанный втаблице, говоритотом, что она могла одержать не более двух побед.
Из сказанного следует, что команда 6в класса одержала две победы и один матч свела вничью, а количество очков распределяется между командами так: 6а — 3, 6в — 1, 6в — 5, 6г — 3.
Ясно, что команда 6б занимает четвертое место, а второе и четвертое места нужно распределить между командами 6а и 6г в зависимости от соотношения забитых и пропущенных шайб.
Так как команды 6а и 6в сыграли вничью (смотри вторую клетку первой строчки), то в первой клетке второй строчки нужно указать тот же счет.
Установим результаты игры 6в со всеми командами. Так как в матче с командой 6г команде 6в забит один гол, то в этом матче ничейный счет 1:1 (два гола нужны команде 6в для двух побед в остальных матчах). Значит, счет 1:1 ставится в четвертой клетке третьей строки и третьей клетке четвертой строки. Теперь ясно, что команда 6в победила команды 6а и 6в со счетом 1:0 в каждом матче, и этот счет нужно указать в первой и второй клетках третьей строки, а в третьей клетке первой строки и третьей клетке второй строки нужно указать счет 0:1.
Теперь очевидно, что команда 6а в матче с командой 6г пропустила одну шайбу, а команда 6г забила одну шайбу. Следовательно, команда 6г проиграла со счетом 1:5, а команда ба выиграла со счетом 5:1 и имеет общий счет 6:3.
Осталось установить счет в матче команд 6в — 6г. Так как в играх с командами 6а и 6в команда 6в пропустила в сумме две шайбы.
Команда 6г в играх с командами 6а и 6в пропустила 6 шайб. Значит, в матче с командой 6б она пропустила одну шайбу.
Из сказанного следует, что в игре между командами 6б и 6г счет был 1:2 и общий счет команды 6б был 2:4, а команды 6г был 4:7.
Из общего счета команд 6а и 6г заключаем, что второе место заняла команда 6а.
Итоговая таблица имеет вид:
***Задача № 8.4. В розыгрыше первенства по футболу встретились футбольные команды: «Авангард», «Буревестник», «Динамо», «Спартак» и «Торпедо». Они сыграли между собой по одному матчу, причем в каждом туре одна из команд была свободна от игры.
В первом туре «Буревестник» проиграл спартаковцам, а во втором — выиграл у «Авангарда».
В третьем туре команда «Торпедо» была свободна от игры, одержав перед этим победу и проиграв другую встречу.
В четвертом туре свободным был «Авангард», имевший в своем активе две победы при трех сыгранных матчах. Динамовцы к этому времени сумели выиграть только один матч.
Каких результатов добилась каждая из команд в соревнованиях, если встречи четвертого и пятого тура окончились вничью?
*** Задача № 8.5. Два стрелка произвели по 5 выстрелов, причем попадания были следующие: 10, 9, 9, 8, 8, 5, 4, 4, 3, 2.
Первыми тремя выстрелами они выбили одинаковое количество очков, но тремя последними выстрелами первый стрелок выбил втрое больше, чем второй.
Определите, сколько очков набрал каждый из них тремя выстрелами.
Глава 9. Числовые ребусы
К числовым ребусам относятся арифметические выражения, в которых все или некоторые цифры заменены символами (буквами, звездочками и т.д.). Чаще всего числовые ребусы представляют собой числовые равенства.
Числовой ребус представляет собой логическую задачу, в которой путем логических рассуждений требуется расшифровать значение символа и восстановить числовую запись.
Имеются некоторые правила шифровки и дешифровки ребусов.
Так, если ребус шифруется буквами, то каждой букве должна соответствовать единственная цифра, а двум различным буквам должны соответствовать две различные цифры. Поэтому, если при дешифровке ребуса найдено цифровое значение одной буквы, то другие буквы это значение принимать не могут.
При шифровке ребуса одним символом (мы будем пользоваться только символом звездочка — *) этим символом шифруются различные цифры.
При дешифровке ребуса часто приходится пользоваться следующими правилами:
- Если в результате умножения некоторого числа на однозначное число получено исходное число, то, очевидно, множитель равен единице.
- Нуль не может быть крайней левой цифрой в числе, а результат умножения на нуль состоит из одних нулей.
- Если в результате умножения некоторого числа, не оканчивающегося нулем, на некоторое однозначное число в числе единиц получен нуль, то число единиц множимого и множителя есть пара чисел, одно из которых равно пяти, а второе — четное.
- Если произведение некоторого k-значного числа на число, большее или равное пяти, дает k-значное число, то ясно, что множимое начинается с единицы.
Подобных особенностей при расшифровке числовых ребусов можно отметить очень много. Они будут выясняться в ходе решения предлагаемых примеров.
Числовые ребусы можно классифицировать по тем арифметическим операциям, которые в них используются. В связи с этим целесообразно рассматривать числовые ребусы следующих видов:
- Числовые ребусы, использующие операции сложения и вычитания.
- Числовые ребусы, использующие операции умножения и деления.
- Числовые ребусы, использующие операцию возведения в степень.
Рассмотрим примеры ребусов каждого из перечисленных классов.
-
Числовые ребусы, содержащие операции сложения и вычитания
При решении задач этого класса наиболее часто приходится пользоваться следующими свойствами операции сложения натуральных чисел.
- Если при суммировании двух k-значных чисел в сумме получается (k+1)-значное число, то его наивысший десятичный знак равен 1.
- Если при суммировании двух одинаковых k-значных чисел в сумме получается k-значное число, то десятичный знак наивысшего разряда слагаемых не превосходит 4.
** Задача № 9.1.
Решение задачи № 9.1. Так как при суммировании двух четырехзначных чисел получается пятизначное число, то Д = 1, а У больше или равняется 5. Очевидно, что А — четное число и А меньше 5 (в противном случае 2А больше 10 и при суммировании чисел сотен мы бы получили нечетное число). В связи с этим 2Д = А и, значит, А = 2. При этом, суммируя десятки, получаем К = 4. Так как при суммировании единиц мы в числе единиц получаем А = 2, то либо Р — 1, либо Р = 6. Но Р ≠ 1, так как Д = 1. Поэтому Р = 6.
При суммировании тысяч мы в числе единиц получаем Р = 6, а так как 2У больше 10, то У = 8 и ребус расшифровывается так:
** Задача № 9.2.
** Задача № 9.3.
Некоторые числовые ребусы, в силу своей конструкции, позволяют применить особые приемы, которые приводят к оригинальному и короткому решению.
Рассмотрим два класса таких задач.
К первому классу отнесем ребусы, в которых слова состоят из одних и тех же слогов,ё но взятых в различных комбинациях. Это дает возможность оперировать каждым слогом как единым числом. Например:
*** Задача № 9.4.
Отметим, во-первых, что П = 1. Далее выделим два слога: «О» и «ЛЕТ». Обозначим ЛЕТ = А. Тогда задача может быть записана так:
Это уравнение имеет единственное решение: О = 7, А = 894, которое может быть найдено путем рассмотрения единичных значений О. Действительно, так как О — однозначное число, то, придавая ему значение из множества {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, мы найдем и десять возможных значений А. Из них целое и, очевидно, трехзначное будет удовлетворять уравнению.
При этом ребус расшифровывается так:
Ко второму классу отнесем ребусы, в которых результат суммирования одинаковых чисел представляет собой число, которое имеет одинаковые десятичные знаки, то есть имеет вид: ααα… α = α · 111..1 и, разлагая число 111…1 на множители, мы получим возможность расшифровать ребус.
Приведем пример такого ребуса.
*** Задача № 9.5.
Решение задачи № 9.5. Так как произведение шестизначного числа «ПЧЕЛКА» на 7 дает шестизначное число «ЖЖЖЖЖЖ», то П = 1, а Ж ≥ 7 .
Рассмотрим возможные значения Ж.
- Пусть Ж = 7. Тогда ПЧЕЛКА = 777777:7 = = 111111, и различные буквы в слове «ПЧЕЛКА» соответствуют одной и той же цифре.
- Пусть Ж = 8. Тогда ПЧЕЛКА = 888888:7 = 126984, и тогда в слове «ПЧЕЛКА» буква «К» имеет то же значение, что и буква «Ж», что противоречит условию задачи.
- Если Ж = 9, то ПЧЕЛКА = 999999 : 7 = = 142857. Этот результат не противоречит условию задачи и, следовательно, Ж = 9, П = 1, Ч = 4, Е = 2, Л = 8, К = 5, А = 7.
2. Числовые ребусы, содержащие операции умножения и деления
Во-первых, рассмотрим класс задач, зашифрованных одним символом — звездочкой. Здесь нет однозначного соответствия между цифрами и этим символом, то есть звездочка может здесь изображать любую из десяти цифр. Поэтому, пользуясь свойствами операций умножения и деления, требуется вместо звездочек найти и подставить цифры.
Рассмотрим ряд таких примеров.
** Задача № 9.6.
Решение задачи № 9.6. Так как при умножении двузначного числа ** на число 8 мы получаем двузначное число, то число десятков множимого должно быть равно 1.
При умножении числа единиц множимого на число 8 мы получаем число, в числе единиц которого стоит цифра 6. Это возможно в двух случаях: или число единиц множимого равно 2, или оно равно 7. Но в последнем случае имеем произведение 17×8 = 136, то есть число трехзначное, а по условию задачи оно должно быть двузначным. Значит, число единиц множимого равно 2, и пример расшифровывается так:
** Задача № 9.7.
Решение задачи № 9.7. Так как произведение множителя на число 7 в числе единиц имеет цифру 6, то множитель равен 8.
Так как произведение трехзначного числа на 8 дает трехзначное число, то число сотен множимого равно 1. Покажем, что число десятков множимого также равно 1. В самом деле, если бы число десятков множимого было бы больше 1, например, 2, то произведение множимого на 8 дало бы четырехзначное число. Значит, пример расшифровывается так:
** Задача № 9.8.
Решение задачи № 9.8. Чтобы при умножении двузначного числа на 8 получить двузначное число, необходимо, чтобы число десятков множимого было равно 1.
Так как произведение двузначного числа с числом десятков равным 1 на 8 дает двузначное число, то число единиц множимого не более двух, то есть либо 0, либо 1, либо 2.
Но произведение этого двузначного числа на число единиц множителя дает трехзначное число. Значит, единиц множителя больше 8, то есть 9, а числом единиц множимого может быть только число 2.
Следовательно, пример расшифровывается так:
*** Задача № 9.9.
*** Задача № 9.10.
Решение задачи № 9.10. Так как произведение делителя на число десятков частного оканчивается цифрой 5, число единиц делителя равно 7, то число десятков частного равно 5.
Так как произведение числа единиц частного на 7 оканчивается цифрой 1, то число единиц частного равно 3. Таким образом, частное равно 53.
Установим число десятков делителя. Оно не может быть равно 1, так как в этом случае произведение 17×5 = 85 — число двузначное, а по условию оно — трехзначное. Оно не может быть равно 3, так как в этом случае произведение 37×3 = 111 — число трехзначное, а по условию оно двузначное. Следовательно, число десятков частного равно 2, делитель равен 27, делимое равно 27×53 = 1431, и ребус расшифровывается так:
*** Задача № 9.11.
Решение задачи № 9.11. Так как произведение двузначного делителя на 8 есть число двузначное, то число десятков делителя равно 1, а число единиц делителя не более 2, то есть или 1, или 2.
Так как произведение числа сотен и числа единиц частного на делитель есть числа трехзначные, то число сотен и число единиц частного больше числа десятков частного, то есть число сотен частного и число единиц частного равны 9, а число единиц делителя равно 2.
Таким образом, делитель равен 12, частное равно 989, а делимое равно 989×12 = 11868, и ребус расшифровывается так:
*** Задача № 9.12.
*** Задача № 9.13.
3. Числовые ребусы, использующие операцию возведения в степень
При решении задач этого класса полезно учитывать следующие свойства степени натуральных чисел.
- Если основание степени оканчивается одним из чисел 0,1, 5, 6, то значение степени с любым натуральным показателем будет оканчиваться тем же числом.
- По числу десятичных знаков основания степени и по показателю степени можно оценить число десятичных знаков значения степени, а по числу десятичных знаков значения степени и по показателю степени можно оценить число десятичных знаков основания степени.
Рассмотрим несколько примеров.
*** Задача № 9.14.
(А А)Н = А Н Н А.
Решение задачи № 9.14. Так как основание степени оканчивается цифрой А , и значение степени оканчивается той же цифрой, то число А может быть одним из чисел: 0, 1, 5, 6.
Очевидно, Н не равно 1. Значит, или Н = 2, или Н = 3 (Н меньше 4, иначе уже 104 — число пятизначное).
Предположим, что Н = 2. Ясно, что А не равно 0. Далее А не равно 1, так как (II)2 = 121 — число трехзначное, а по условию оно должно быть четырехзначным. А не равно 5, так как (55)2 = 3025 и, значит, значение степени не удовлетворяет условию задачи. А не равно 6, так как (66)2 = 4356 также не удовлетворяет условию задачи. Следовательно, Н не равно 2. Пусть Н = 3. Так как (22)3 = 10648 — число пятизначное, то А меньше 2 и, следовательно, А = 1, и ребус расшифровывается так:
(11)3 = 1331.
*** Задача № 9.15.
М3 = К У Б.
*** Задача № 9.16. Число 19 * 83 — точный куб. Найти его.
Решение задачи № 9.16. Так как (20)3 = 8000, а(30)3 = 27000, то ясно, что основание степени X заключено между числами 20 и 30.
Так как третья степень числа X оканчивается цифрой 3, то число X имеет в числе единиц цифру 7(73 = 343). Значит, X = 27, а (27)3 = 19683.
Задача № 9.17.
**198 * 7 — это пятая степень некоторого числа. Найти число.
Решения задач
Решение задачи № 1.3. Перевоз животных и капусты с левого берега реки на правый можно обеспечить с сохранением капусты и всех животных следующим образом:
В первом рейсе перевозчик берет с собой козу и собаку, оставляя на левом берегу двух волков и капусту. Переехав на правый берег, перевозчик оставляет там козу и с собакой возвращается на левый берег.
Во втором рейсе перевозчик берет с собой собаку и капусту, оставляя на левом берегу только двух волков. Переехав на правый берег, перевозчик оставляет там собаку и капусту, а с козой возвращается на левый берег.
В третьем рейсе перевозчик берет с собой двух волков, оставляя на левом берегу козу. Переехав на правый берег, он оставляет там двух волков и капусту, берет с собой собаку и возвращается на левый берег.
В четвертом рейсе перевозчик забирает с собой собаку и козу и переезжает на правый берег.
На этом перевоз закончен.
Решение задачи № 2.2. Обозначим число попаданий в «пятерку» через х, а в «семерку» — через у. Тогда из условия задачи следует равенство:
5 · х + 7 · у + 40 = 76.
Из этого равенства приходим к уравнению с двумя неизвестными:
5х + 7у = 36.
Так как последнее уравнение необходимо решить в целых положительных числах, то для этого, очевидно, достаточно перебрать целые значения х от 1 до 8, выясняя каждый раз, будет ли при этом целым числом значение у.
Нетрудно показать, что уравнение имеет в целых числах единственное решение:
х = 3, у = 3.
Решение задачи № 2.3. Учитывая, что у школьника были монеты только достоинством 15 копеек и 20 копеек, и за билет в кино он отдал две монеты, имеем три возможных варианта траты денег при покупке билета:
- 15 + 15 = 30 коп.,
- 15 + 20 = 35 коп.,
- 20 + 20 = 40 коп.
Так как стоимость билета в кино составляла 1/5 часть денег школьника, то имеем три возможных варианта суммы всех денег школьника:
- 150 коп., 2. 175 коп., 3. 200 коп.
После оплаты билета в кино у него осталась одна из трех возможных сумм денег:
- 120 коп., 2. 140 коп., 3. 160 коп.
Половину этих денег составляют суммы:
- 60 коп., 2. 70 коп., 3. 80 коп.
Так как половину оставшихся денег школьник отдал за обед, оплатив его тремя монетами, то это возможно лишь в одном из трех случаев, когда половина оставшихся денег есть сумма в 60 копеек. Отсюда ясно, что у школьника было 150 копеек. Их распределение по достоинствам монет могло быть таким:
- 15 + 15 + 20 + 20 + 20 + 20 + 20 ,
- 15 + 15 + 15 + 15 + 15 + 15 + 20 + 20,
- 15 + 15 + 15 + 15 + 15 + 15 + 15 + 15 + 15 + 15.
Но из условия задачи двадцатикопеечных монет больше. Значит, имеем первый случай.
Решение задачи № 2.4. Обозначим через а, результат 1-го выстрела Пети. Тогда по условию задачи
а2 + а3 + а4 + а5 = 7 а5 .
Так как в круг «10» попали по одному разу и Петя, и Боря, то наибольшее число очков, которое можно выбить четырьмя выстрелами, равно
12 + 11 + 10 + 9 = 42.
Так как по условию задачи а, не может быть равным «6», то а, = 5 и, следовательно,
а2 + а3 + а4 + а5 = 35.
Известно, что одно из чисел а2, а3, а4, а5 равно 10. Пусть а2 = 10. Тогда а3 + а4 + а5 = 25.
Если бы Петя одним из выстрелов попал в круг «12», например, а3 = 12, то а4 + а5= 13, а это невозможно.
Следовательно, в круг «12» попал Боря.
Решение задачи № 2.5. Пусть в стаде было х = 10 · k + n баранов. Здесь k — число десятков баранов, а n — число единиц баранов в стаде. Тогда братья за проданных баранов выручили х · х рублей, то есть (10k+n)(10k+n) рублей. Но число (10 · k + n) · (10 · k+n)=100 · k2 +
+ 20 · k · n + n2.
Ясно, что число 100 · k2 + 20 · k • n содержит четное число десяток, и поэтому при дележе этого числа братьям досталось одинаковое число десяток.
Так как в итоге дележа число десяток оказалось нечетным, то это могло произойти лишь за счет числа n1. Ясно, что n больше четырех. Но при n = 4, n2 = 16; при n = 5, n2 = 25; при n = 6, n2 = 36; при n = 7, n2 = 49; при n = 8, n2 = 64; при n = 9, n2 = 81.
Следовательно, n2 содержит нечетное число десяток в двух случаях: при n = 4 и при n = 6. В обоих случаях число n2 оканчивается цифрой 6. Значит, младшему брату не хватило до 10 рублей (в последний момент деления денег) четырех рублей. Старший брат должен был компенсировать ему 2 рубля. Следовательно, нож стоил два рубля.
Решение задачи № 3.1. Цвет надетого на гнома капюшона может определить каждый из двух гномов, на которых надеты синие капюшоны. Действительно, каждый из гномов, на которых надеты синие капюшоны, видит перед собой четырех гномов, из которых трое в красных капюшонах (а красных капюшонов всего 3), и поэтому сразу же придет к выводу о том, что на нем может быть только синий капюшон (см. рисунок).
Решение задачи № 3.2. Цвет надетого на гнома капюшона может определить каждый из пяти гномов, участвующих в игре.
Действительно, им показали 3 красных и 4 синих капюшона, а в темноте надели 2 красных и 3 синих капюшона (см. рисунок).
Так как каждый из трех гномов в синих капюшонах видит перед собой два красных капюшона и знает, что всего красных три, то он может рассуждать так:
«Если бы на мне был красный капюшон, то каждый из двух оставшихся в синих капюшонах гномов видел бы три красных капюшона (а их всего 3) и пришел бы к выводу, что на нем синий. Но они молчат. Значит, на мне не красный, а синий капюшон».
Так как каждый из двух гномов в красных капюшонах видит перед собой один красный и три синих капюшона и знает, что всего синих четыре, то он может рассуждать так:
«Если бы на мне был синий капюшон, то оставшийся гном в красном капюшоне видел бы четыре синих капюшона (а их всего 4) и пришел бы к выводу, что на нем красный. Но он молчит, значит, на мне не синий, а красный капюшон».
Решение задачи № 3.3. Ни один из трех гномов, фигурирующих в задаче, не может определить цвет надетого на него капюшона.
Решение задачи № 3.4. Цвет своего капюшона может определить каждый из двух гномов, на которых надели капюшоны синих цветов.
Действительно, всего в игре участвует 8 гномов. На них надето 4 красных, 2 синих и 2 белых капюшона, а спрятан один красный и два синих капюшона (см. рисунок).
Каждый из двух гномов, на которых надеты синие капюшоны, может рассуждать двояко:
- Пусть на мне капюшон красного цвета. Тогда гномы в капюшонах не красного цвета видят перед собой 5 гномов в капюшонах красного цвета (а капюшонов красного цвета всего 5). Следовательно, гномов в капюшонах красного цвета можно исключить из рассмотрения и тогда передо мной остается три гнома: один в капюшоне синего цвета и два — в капюшонах белого цвета. Но белых капюшонов всего 2, значит, гном в синем капюшоне однозначно определяет синий цвет своего капюшона и оповещает об этом участников игры, а я узнаю, что на мне, действительно, красный капюшон.
- На мне капюшон не красного цвета. Тогда исключаем из рассмотрения 4-х гномов в красных капюшонах. Остается четыре гнома: два в белых капюшонах и два в синих капюшонах. Любой из гномов в синем капюшоне видит перед собой двух гномов в белых капюшонах. Но белых капюшонов всего 2. Поэтому любой гном в синем капюшоне приходит к правильному выводу о синем цвете своего капюшона.
Таким образом, цвет надетого на гнома капюшона может определить один из гномов в синем капюшоне.
Решение задачи № 4.2. Предположим, что первое утверждение первого болельщика верно (Аня заняла второе место1). При этом, очевидно, будут ложными второе утверждение второго болельщика (Валя заняла второе место) и первое утверждение третьего болельщика (Галя заняла второе место). Значит, будет верным первое утверждение второго болельщика (Аня заняла первое место Г Подчеркнутые утверждения приводят к противоречию: Аня заняла первое и второе места одновременно.
Предположим теперь, что верно второе утверждение первого болельщика (Даша заняла третье место). При этом ложными будут первое утверждение первого болельщика и второе утверждение третьего болельщика. Отсюда следует, что верно первое утверждение третьего болельщика (Галя заняла второе место) и ложно второе утверждение второго болельщика. Но тогда верным является первое утверждение второго болельщика (Аня заняла первое место). При этом ясно, что Валя заняла четвертое место.
Выделенные курсивом утверждения дают ответ на вопрос задачи.
Решение задачи № 4.3. Установим имена братьев, сказавших правду.
- Предположим, что Толя сказал правду. Тогда сказали неправду Андрей, Витя (про них Толя сказал, что они говорят неправду) и Дима, который возражает Толе.
Таким образом, сказавших неправду будет больше двух, а это противоречит условию задачи. Следовательно, Толя говорит неправду.
- Предположим, что Дима говорит правду. Тогда неправду сказали Толя, один из первых двух братьев (это утверждает Дима) и Юра, который возражает Диме.
Вновь приходим к противоречию. Следовательно, Дима сказал неправду.
Значит, правду сказали Андрей, Витя и Юра. Но из высказываний Андрея и Вити следует, что окно разбил Толя.
Решение задачи № 4.4. Чтобы выяснить, к какому племени принадлежит проводник (к пришельцам или аборигенам), нужно установить, каков ответ мог дать проводнику встречный житель острова.
Легко видеть, что ответ встречного жителя острова мог быть только один: «Я — абориген». Этот ответ является правдой для аборигена и ложью для пришельца. Следовательно, проводник сказал путешественнику правду, и поэтому он принадлежит к племени аборигенов.
Решение задачи № 4.5. Запишем высказывания Косоглаза и Бороды в виде таблицы, в которой учтен номер высказывания каждого из них:
| №№
выска- зывания |
Высказывания
Косоглаза |
Высказывания
Бороды |
| 1 | Борода — чередовец | Косоглаз — чередовец |
| 2 | Курнос — правдовец | Курнос — лгуновец |
| 3 | Алощек — чередовец | Алощек — правдовец |
| 4 | Длинноух — лгуновец | Длинноух — чередовец |
Рассмотрим все возможные варианты принадлежности Бороды и Косоглаза к жителям деревень Правдино, Чередово и Лгуново.
- Они не могут быть оба жителями Правдино, так как это противоречит их первым высказываниям.
- Невозможна принадлежность одного из них и к жителям деревни Правдино, а второго — к жителям деревни Лгуново, так как иначе в одном из первых высказываний один из них назывался бы жителем деревни Лгуново.
- Невозможна принадлежность одного из них к жителям деревни Правдино, а второго — к жителям деревни Чередово, так как иначе хотя бы по одному из трех их высказываний (2-го, 3-го и 4-го) совпадали.
- Они не могут быть оба жителями деревни Чередово, иначе из совпадения их первых высказываний (они в этом случае истинны) должно следовать совпадение третьих высказываний (а этого нет).
- Невозможна принадлежность одного из них к жителям деревни Чередово, а второго к жителям деревни Лгуново, так как иначе хотя бы по одному из трех высказываний (2-го, 3-го и 4-го) совпадали, то есть оба были ложны.
Значит, в единственно возможном варианте они оба являются жителями деревни Лгуново. При этом из их вторых высказываний следует, что Курнос — чередовец, из третьих высказываний следует, что Алощек — лгуновец, а из четвертых высказываний следует, что Длинноух — правдовец.
Решение задачи № 5.3. Здесь воспользуемся таблицей 4×4 вида:
| Жидкости | Сосуды | |||
| Бутылка | Стакан | Кувшин | Банка | |
| Молоко | ||||
| Квас | ||||
| Лимонад | ||||
| Вода | ||||
Так как вода и молоко не в бутылке, то следует поставить знак — в клетках L14 и L11.
Так как сосуд с лимонадом стоит между кувшином и сосудом с квасом, то лимонад и квас не в кувшине. Значит, знак — нужно поставить в клетках L32 и L33.
Так как в банке не лимонад и не вода, то знак — следует поставить в клетках L43 и L44.
Так как стакан стоит между банкой и сосудом с молоком, то молоко не в стакане и не в банке. Значит, знак – нужно поставить в клетках L21 и L41.
При этом таблица принимает вид:
| Жидкости | Сосуды | |||
| Бутылка | Стакан | Кувшин | Банка | |
| Молоко | – | – | – | |
| Квас | – | |||
| Лимонад | – | – | ||
| Вода | – | – | ||
Учитывая наличие взаимно однозначного соответствия между множеством сосудов и множеством жидкостей, можно поставить знак + в клетках L31, и L42, а знак – поместить в клетках L34, L12, L22.
При этом, очевидно, знак + ставится в клетках L13 и L24, и мы получаем таблицу, дающую решение.
| Жидкости | Сосуды | |||
| Бутылка | Стакан | Кувшин | Банка | |
| Молоко | – | – | + | – |
| Квас | – | – | – | + |
| Лимонад | + | – | – | – |
| Вода | – | + | – | – |
Из этой таблицы следует, что молоко находится в кувшине, квас — в банке, лимонад — в бутылке, вода — в стакане.
Решая эту задачу с помощью графика, мы получим ее решение в виде:
Решение задачи № 5.5. Будем изображать тремя кругами множества подруг, туфель и платьев, а их элементы — точками.
Так как Наташа была в зеленых туфлях, то соединим сплошной линией элементы множеств «Наташа» — «зеленые туфли», а пунктирными линиями — элементы множеств «Валя» — «зеленые туфли» и «Аня» — «зеленые туфли».
Так как ни туфли, ни платье Вали не были белыми, то соединим элементы множеств «Валя» — «белые туфли», «Валя» — «белое платье» пунктирными линиями. Теперь ясно, что Валя была в синих туфлях, а Аня — в белых, и, значит, нужно соединить сплошными линиями элементы множеств «Валя» — «синие туфли», «Аня» — «белые туфли».
Так как у Ани цвета платья и туфель совпадали, то Аня была в белом платье.
Так как у Вали и Наташи цвета туфель не совпадали, то Наташа была в синем платье, а Валя — в зеленом. Следовательно, остается соединить сплошными линиями элементы множеств: «Аня» — «белое платье», «Наташа» — «синее платье» и «Валя» — «зеленое платье», а график, дающий решение задачи, будет иметь вид:
Решение задачи № 6.2. Множество мест волейбольных команд в результатах соревнования упорядочено. Поэтому элементы этого множества можно изображать на прямой по мере возрастания номеров мест справа налево.
Так как команда А отстала от команды Б на три места, а команда Е опередила Б, но отстала от Д, то команды А, Б, Е и Д расположены в порядке:
то есть впереди Д, за ней Е , за Е идет команда Б и последней — команда А. Причем между командами А и Б находятся две команды В и Г.
Так как команда В оказалась между командами Г и Д, то это возможно лишь в случае, если команда В идет за командой Б, а команда Г идет за командой В.
Таким образом, на первом месте команда Д, на втором — Е, на третьем — Б, на четвертом — В, на пятом — Г и на шестом — А.
Решение задачи № 6.3. Установим возраст Бори. Ясно, что в детский сад ходит пятилетний ребенок и по условию задачи это девочка. Значит, Боре больше пяти лет.
Так как Аня старше Бори, то Боре не может быть пятнадцать лет. Следовательно, Боре или 8 лет, или 13.
Сумма лет Ани и Веры делится на 3. С учетом возраста детей в семье это возможно в двух случаях:
- Одной девочке 5 лет, а второй — 13.
- Одной девочке 8 лет, а второй — 13.
В обоих случаях одной девочке 13 лет. Следовательно, Боре не 13 лет. Значит, Боре 8.
Теперь установим возраст каждой девочки.
Сумма лет Ани и Веры делится на три, и это возможно в случае, когда одной девочке 5 лет, а второй 13. Но по условию задачи Аня старше Бори. Поэтому Ане 13 лет, а Вере 5. При этом ясно, что Гале 15 лет.
Решение задачи № 6.4. До разбития участников катания на пары построим их по росту. Изобразим такое построение цепочкой кружков, вписывая инициалы участников катания в кружки. Учитывая условия задачи, получим цепочку:
Из этой цепочки ясно, что:
- Юра Воробьев должен кататься с Люсей Егоровой, иначе Люся Егорова останется без партнера, рост которого выше роста Люси.
- Андрей Егоров должен кататься с Олей Петровой, иначе Оля останется без соответствующего партнера.
- Саша Петров должен кататься с Инной Крымовой, в противном случае он будет кататься с Аней Воробьевой, а Инна Крымова останется со своим братом Димой Крымовым, что противоречит условию задачи.
- Наконец, Дима Крымов должен кататься с Аней Воробьевой.
Таким образом, образуются следующие пары:
А.Е. О.П.
Ю.В. Л.Е.
С.П. И.К.
Д.К. А. В.
Решение задачи № 6.5. Будем обозначать места расположения девочек кругами, занумеровав круги по ходу часовой стрелки.
Предположим, что в первом круге стоит девочка в зеленом платье. По условию задачи это не Аня, не Валя и не Надя. Значит, в зеленом платье — Галя.
Известно, что Галя стоит между девочкой в голубом платье и Надей. Будем считать, что в четвертом круге стоит девочка в белом платье (это не Надя), но тогда по условию задачи в первом круге должна стоять либо Валя, либо девочка в розовом платье. Это противоречит тому, что в первом круге стоит Галя, одетая в зеленое платье. Следовательно, девочка в белом платье стоит в третьем круге. При этом девочкой в голубом платье должна быть Валя, а Надя должна быть в розовом платье.
Теперь ясно, что Аня — в белом платье.
Галя — платье зеленое
Надя, платье розовое,
Аня, платье белое,
Валя, платье голубое
Решение задачи № 6.7. Будем изображать кабины колеса обозрения в виде прямоугольников и в них записывать имена катающихся, указывая для детей имена их отцов, а для отцов — имена их детей. Тогда, используя условия задачи, будем иметь следующую схему:
Так как Алексей Иванович — не отец Лени (он с ним катается), не отец Андрея (с отцом Андрея катался Тима), не отец Коли (с отцом Коли катался Андрей), то Алексей Иванович — отец Тимы.
Так как Леня катался с отцом Тимы, Андрей — с отцом Коли, а Коля — с отцом Андрея, то Коля катался с отцом Лени.
Так как Тима — сын Алексея Ивановича, то Валентин Петрович катался с Тимой. Но Тима катался с отцом Андрея, значит, Андрей — сын Валентина Петровича.
Так как Андрей — сын Валентина Петровича, то Андрей катался с Федором Семеновичем. Но Андрей катался с отцом Коли. Значит, Федор Семенович — отец Коли.
Теперь ясно, что Коля катался с Григорием Аркадьевичем. Но Коля катался с отцом Лени, значит, Григорий Аркадьевич — отец Лени.
Ответы на все вопросы задачи можно изобразить в виде следующей схемы:
Решение задачи № 6.9. Будем обозначать места юношей в цепочке влюбленных кружками, а места девушек— квадратами и в них будем записывать имена влюбленных.
В силу условий задачи вся группа влюбленных представляет собой одну замкнутую цепь, звенья которой расположены в определенном порядке. Занумеруем их по ходу часовой стрелки.
Предполагается, что в этой цепочке юноша, занимающий место в круге 1, влюблен в девушку, занимающую место в квадрате 2, а девушка, занимающая место в квадрате 2, влюблена в юношу, занимающего место в круге 3 и т.д.
Не нарушая общности рассуждений, предположим, что место в круге 1 занимает Коля, тогда по первому условию задачи место в квадрате 4 занимает Таня.
Рассмотрим возможные варианты размещения остальных участников группы. Здесь возможны два случая:
1) Петя занимает место в круге 5, а Юра занимает место в круге 3.
2) Петя занимает место в круге 3, а Юра занимает место в круге 5.
Но в первом случае по условию 2 Зина занимает место в квадрате 2 и, следовательно, она влюблена в Юру, что противоречит условию 3 и, значит, первый случай возможен.
Во втором случае Зина занимает место в квадрате 6 и, значит, Галя занимает место в квадрате 2. Такое размещение влюбленных не противоречит условиям задачи. Решение может быть изображено на следующей схеме:
Таким образом, Коля влюблен в Галю, Галя — в Петю, Петя — в Таню, Таня — в Юру, Юра — в Зину и Зина — в Колю.
Решение задачи № 7.2. Расположим камни в ряд, выделив два первых камня, а затем три группы камней по четыре в каждой:
Выигрышная стратегия игры начинающего в этом случае незначительно отличается от выигрышной стратегии начинающего, описанной в задаче № 7.1.
Действительно, для выигрыша начинающий своим первым ходом должен взять два камня, а затем после каждого хода противника, взявшего из очередной четверки камней один, два или три камня, брать оставшиеся. При этом, очевидно, он возьмет и последний камень.
Если начинающий допустит ошибку в одном из своих ходов, то противнику для выигрыша необходимо поступить так, как это описано в задаче № 7.1.
Решение задачи № 7.3. Если в первой кучке 30 камней, а во второй — 16 (неравное количество), то, взяв своим первым ходом из первой кучки 14 камней (уравнивая кучки), начинающий обеспечивает себе выигрыш. Действительно, в дальнейшем ходе игры начинающему достаточно брать из кучки столько же камней, сколько из второй кучки взял противник своим последним ходом. Ясно, что при такой стратегии последний камень возьмет начинающий и, значит, выиграет.
При условии, что в каждой кучке по 15 камней, выиграет противник, если он будет придерживаться в игре стратегии, описанной в предыдущем случае после уравнивания кучек.
Решение задачи № 7.4. Легко видеть, что противник всегда выиграет, если он будет после каждого хода начинающего первой пуговицей переносить вторую пуговицу на то же поле, на которое перенес первую пуговицу начинающий.
В результате такой игры начинающий первым достигнет крайнего правого поля. После этого предстоит ход начинающего, а ему уже некуда ходить.
Решение задачи № 7.5. Если пуговицы три, то начинающий может своим первым ходом передвинуть одну из пуговиц вправо на последнее поле, и тогда игроки оказываются в рассмотренной ситуации для двух пуговиц. При этом предстоит ход противника. Следовательно, начинающий в итоге игры будет иметь последний ход, после которого противнику некуда будет ходить.
Решение задачи № 7.6. В этой игре выигрывает начинающий, если он своим первым ходом поставит свой знак («крестик» или «нолик» в центре доски).
Действительно, пусть начинающий поставит в центре доски своим первым ходом, например, «крестик».
После этого хода начинающего противник должен будет поставить «нолик» или в одну из угловых клеток, или в среднюю (боковую) клетку.
Если после этого начинающий поставит «нолик» в клетку, симметричную той, что занята противником, то при любом ходе противника начинающий выигрывает, как это видно из следующих рисунков:
Решение задачи № 7.7. Проигрывает начинающий. Выигрывает противник, если он будет ставить свои ладьи симметрично ладьям первого мальчика относительно центра доски.
Решение задачи № 7.9. Выигрышную стратегию имеет начинающий. Действительно, начинающий первым называет число 1, а в дальнейшем, после того как противник назовет число k, (не больше 10), называет число 11 – k1(i = 1, 2, 3, … , 9).
Тогда в итоге будет названа сумма:
1 + k1 + (11 – k1) + k2+(11 – k2) +… + k9 + (11 – k9 ) =
= 1 + (k1 + k2 +… + k9) + 9 · 11 – (k1 + k2+ … + 91) =
= 1+9 · 11 = 100.
Причем числа 100 достигнет начинающий, так как он последний назовет число 11 – k9 добавление которого к предыдущей сумме и даст число 100.
Решение задачи № 8.2. Для решения задачи № 8.2 воспользуемся шахматной турнирной таблицей.
Используем условия задачи и внесем их в таблицу.
Так как А сыграл все партии вничью, то во всех клетках строки А и столбца А следует поставить по 0,5.
Так как В проиграл Б, то следует поставить 1 в клетке на пересечении строки Б со столбцом В и 0 — в клетке на пересечении строки В со столбцом Б.
Так как Г выиграл у Д, то следует поставить 1 в клетке на пересечении строки Г со столбцом Д и 0 — в клетке на пересечении строки Д со столбцом Г.
Результаты остальных игр установим путем логических рассуждений. С этой целью, в первую очередь, выясним, кто занял первое место.
Это не А (по количеству очков он не может быть победителем).
Это не Б (Б сыграл вничью с победителем).
Это не В, так как у него не более 2,5 очков.
Это не Д, так как у него не более 1,5 очков (он не выиграл ни одной партии, а одну — проиграл).
Это Г. Действительно, он имеет две победы (в играх с Д и с занявшим четвертое место) и имеет две ничьи (с А и с Б). Ясно, что Г имеет 3 очка, а В занял IV место.
Установим участника турнира, занявшего последнее (пятое место).
Это, очевидно, не А. Это не Б, так как он сыграл вничью с занявшим последнее место. Это не В (В занял четвертое место). Это не Г (он — победитель).
Следовательно, пятое (последнее) место занял Д. У него две ничьих (с А и Б), у него проигрыш от Г. Остается установить результат игры между В и Д. Д не мог выиграть у В, так как Д не выиграл ни одной партии. Он не мог сыграть с В вничью, так как в этом случае он имел бы 1,5 очка, а В, занявший четвертое место, — только одно очко. Поэтому единственно возможно только то, что В выиграл у Д.
Решение задачи № 8.2 дается итоговой турнирной шахматной таблицей.
Решение задачи № 8.4. Результаты решения задачи будем фиксировать в двух таблицах.
В первую таблицу внесем данные о распределении Hip команд по турам. Эта таблица имеет вид:
Из условия задачи следует, что в третьем туре была свободна от игры команда «Торпедо», а в четвертом — «Авангард».
Так как в первом туре играли команды «Буревестник» и «Спартак», то ни одна из них не могла быть свободной от игры. Следовательно, в первом туре не играла команда «Динамо».
Аналогично устанавливается, что во втором туре свободной от игры была команда «Спартак», а в пятом — «Буревестник».
Выпишем пары команд соперников в каждом туре. В условии задачи сказано, что в первом туре «Буревестник» проиграл спартаковцам и известно, что свободной от игры была команда «Динамо», но тогда очевидно, что второй парой игравших команд были «Торпедо» и «Авангард».
Во втором туре «Буревестник» выиграл у «Авангарда», свободной от игры была команда «Спартак». Значит, второй парой игравших команд были «Торпедо» и «Динамо».
В третьем туре свободной от игры была команда «Торпедо».
Как указывалось, в первом туре «Буревестник» встретился в матче со «Спартаком», во втором — с «Авангардом». Поэтому в третьем туре «Буревестник» играл с «Динамо», а «Авангард» — со «Спартаком».
Наконец ясно, что в четвертом туре «Буревестник» встречался с «Торпедо», «Динамо» со «Спартаком», в пятом же туре между собой сражались команды «Авангард» и «Динамо», а также «Торпедо» и «Спартак».
Следовательно, таблица распределения игр команд по турам имеет вид:
Рассмотрим теперь турнирную таблицу футбольного матча.
По условию задачи все встречи IV-ro и V-ro туров закончились вничью, то есть вничью сыграли команды:
«Буревестник» — «Торпедо»,
«Динамо» — «Спартак»,
«Авангард» — «Динамо»,
«Торпедо» — «Спартак».
Кроме того известно, что в первом туре «Буревестник» проиграл спартаковцам, «Буревестник» выиграл у «Авангарда» во втором туре.
Так как «Авангард» к IV-му туру имел две победы при трех сыгранных матчах и, значит, только одно поражение (во втором туре от «Буревестника»), то «Авангард» выиграл в первом туре у «Торпедо» и в третьем туре — у «Спартака».
Так как команда «Торпедо» к третьему туру имела одну победу и одно поражение (в первом туре от «Авангарда»), то во втором туре «Торпедо» выиграло у «Динамо».
Так как динамовцы к четвертому туру сумели выиграть только один матч, то, очевидно, это была победа над «Буревестником» в третьем туре и поражение от «Торпедо» во втором.
По всем указанным результатам можно заполнить итоговую таблицу футбольного матча.
Решение задачи № 8.5. Решение этой турнирной задачи не требует использования турнирной таблицы. Здесь достаточно произвести элементарные подсчеты.
Обозначим через ар — число очков, которое выбил первый стрелок при р-ом выстреле, а через bр — число очков, которое выбил второй стрелок при р-ом выстреле.
Тогда из условия задачи следуют два равенства:
а, + а2 + а3 = b1 + b2 + b3 (1)
а3 + а4 + а5 = 3 · (b3 + b4 + b5). (2)
Из приведенных попаданий в мишень заключаем, что равенство (2) может выполняться, если b3, b4 и b5 — минимальные по числу очков попадания, а а3, а4, а5 — максимальные по числу очков попадания, и сумма а3 + а4 + а5 кратна трем.
Отсюда видно, что b3, b4, b5 — это числа 2, 3 и 4, а а3, а4, а5 — это числа 10, 9, 8.
Далее видим, что первыми четырьмя выстрелами (каждый стрелок сделал по два выстрела) они выбили очки: 9, 8, 5, 4.
Используем условие (1). Очевидно, что при этом сумма а1 + а2 должна быть наименьшей при ее выборе из четырех чисел (9, 8, 5, 4), а b1, + b2 — максимальной при выборе ее из тех же чисел. Это возможно при а, = 5, а2 = 4, а3 = 10, b1 = 9, b2 = 8, b3= 2.
Таким образом, первый стрелок третьим выстрелом набрал 10 очков, а второй стрелок — 2 очка.
Решение задачи № 9.2.
ВОБЛА
+
ВОБЛА
_______
ПЛОТВА
Так как сумма двух пятизначных чисел равна шестизначному числу, то П = 1.
Так как сумма А + А дает в числе единиц цифру А, то А = 0.
Так как буква О не равна нулю (А = 0) и при суммировании числа тысяч их сумма в числе единиц дает ту же цифру, то О = 9, а Б больше или равна 5.
Так как число единиц А равно нулю, то, суммируя десятки, мы получаем четное число Б. Как видно из суммирования десятков тысяч, В больше 5. Значит, или В = 6, или В = 8. При этом, учитывая суммирование числа тысяч, видим, что Л — нечетное. Это возможно, если Л = 3 и В = 6 или Л = 9 и В = 8. Но Л не равно 9, так как О равно 9. Значит, Л равно 3 и В = 6.
Остается определить значения букв Б и Т.
Суммируя числа сотен, при условии, что Л меньше 5, получаем 2Б = 10 + Т.
Так как Б больше или равно 5, то Б может принимать значения из множества {5,6,7,8,9}. Но Б не может быть равно 5 (иначе Т = А = 0); Б не может быть равно 6, так как В равно 6; Б не может быть равно 8 (иначе Т = В = 6); Б не может быть равно 9, так как О равно 9. Следовательно, Б = 7, Т = 4, и ребус расшифровывается так:
Решение задачи № 9.3.
Как и в задаче № 9.2 находим А = О, О = 9.
Очевидно, справедливы равенства:
К + Л = 10 + Д
2К + 1 = В
Так как при суммировании двух четырехзначных чисел в сумме получается четырехзначное число, то К меньше или равно 4. Но К не равно нулю, так как А = 0; К не может быть равно 4 (иначе из второго равенства получаем В = О = 9).
Пусть К = 1. Тогда из второго равенства следует, что В = 3, а первое равенство принимает вид: Л = Д + Д. Но это возможно лишь при условии, что Д = А = 0 и Л = О = 9.
Пусть К = 2. Тогда В = 5, а первое равенство принимает вид: Л = 8 + Д. Но Д не равно нулю, так как А = 0; Д не равно 1 (иначе Л = О = 9). Значит, К не равно 2.
При К = 3 из второго равенства следует, что В = 7, а первое равенство принимает вид Л = 7 + Д. Но Д не может быть равно нулю, так как А = 0; Д не может быть равно 2 (иначе Л = О = 9). Следовательно, единственно возможно, Д = 1, Л = 8, и ребус расшифровывается так:
Решение задачи № 9.9.
Так как произведение числа единиц множимого на число единиц множителя оканчивается цифрой 6, то числом единиц множителя может быть либо 1, либо 6.
Так как произведение множимого на число десятков множителя есть число четырехзначное, то числом десятков множителя может быть либо 8, либо 9.
Таким образом, множителем может быть одно из четырех чисел: 81, 86, 91, 96.
Легко убедиться, что только число 81 удовлетворяет условию задачи и, следовательно, ребус расшифровывается так:
Решение задачи № 9.12.
Ясно, что произведение числа единиц частного на число единиц делителя равно 8, а это возможно лишь в случае, если число единиц делителя равно 4.
Так как произведение трехзначного делителя на 7 дает трехзначное число, то число сотен делителя равно 1. Следовательно, делителем является число 124.
Так как произведение делителя на 7 дает число трехзначное, а произведение делителя на число десятков частного дает число четырехзначное, то число десятков частного больше 7. Но произведение 124 × 8 = 992 есть число трехзначное, значит, число десятков частного равно 9, а частным является число 97.
При этом делимое равно 124 × 97 = 12028, и ребус расшифровывается так:
Решение задачи № 9.13.
Так как произведение двузначного делителя на 7 есть число двузначное, то число десятков делителя равно 1.
Так как произведение числа единиц частного на делитель оканчивается цифрой 7, то произведение числа единиц делителя на число единиц частного равно 27, то есть произведению 9 × 3 = 27. Но число единиц делителя не может быть равно 9, так как иначе 19 × 7 = 133 есть число трехзначное.
Значит, число единиц делителя равно 3, делитель равен 13, а число единиц частного равно 9.
Так как на втором этапе деления сносится две цифры, то вторая цифра частного равна 0.
Из самой структуры деления видно, что произведение делителя на первую цифру частного и произведение делителя на третью цифру частного равны. Поэтому третья цифра частного равна 7, частное равно 7079, а делимое равно 7079 × 13 = 92027, и ребус расшифровывается так:
Решение задачи № 9.15.
М3 = К У Б.
Так как 43 = 64 — число двузначное, а 103 = 1000 — число четырехзначное, то искомое число М принадлежит множеству {5, 6, 7, 8, 9}. Но кубы чисел 5, 6 и 9 оканчиваются теми же числами, то есть для них М = Б.
Следовательно, или М = 7, или М = 8. Но 73 = 343, то есть здесь К = Б, а равенство 83 = 512 удовлетворяет условию задачи.
Таким образом,
М = 8, К = 5, У = 1, Б = 2.
Решение задачи № 9.17.
* * 198 * 7 — это пятая степень некоторого числа. Найти число.
Так как (20)5 = 3200000 — число семизначное, а (30)5 = 24300000 — число восьмизначное, то искомое число двузначно и меньше числа 30.
Но пятая степень числа X оканчивается тем же числом лишь для X = 7. Следовательно, искомое двузначное число меньше 30 и имеет в числе единиц число 7.
Этим требованиям удовлетворяют только два числа: 17 и 27.
Но легко проверить, что условию задачи удовлетворяет только число 17 и, следовательно,
(17)5 = 1419857.
Ответы
1.1. Организация переправы описана в решении задачи.
Переправу можно осуществить за 20 рейсов.
1.2. Организация перевоза описана в решении задачи.
Для перевоза через реку всех животных и капусты нужно осуществить 4 рейса.
1.3. Организация перевоза описана в решении задачи.
Для перевоза через реку всех животных и капусты нужно осуществить 4 рейса.
2.1. Все головы и хвосты Иван-царевич срубит Змею Горынычу за 9 ударов.
2.2. При стрельбе Алеши по мишени попаданий в «пятерку» и «семерку» было по 3.
2.3. У школьника было вначале 8 монет (две пятнадцатикопеечных и шесть двадцатикопеечных).
2.4. В круг «12» попал Боря.
2.5. Нож стоил два рубля.
3.1. Цвет надетого на гнома капюшона может определить каждый из двух гномов, на которых надеты синие капюшоны.
3.2. Цвет надетого на гнома капюшона может определить каждый из пяти гномов, участвующих в игре.
3.3. Ни один из трех гномов, фигурирующих в задаче, не может определить цвет надетого на него капюшона.
3.4. Цвет своего капюшона может определить каждый из двух гномов, на которых надели капюшоны синих цветов.
4.1. Леня учится в школе № 8, Петя — в школе № 30, а Коля — в школе № 24.
4.2. Аня заняла первое место, Галя — второе, Даша — третье, Валя — четвертое.
4.3. Окно разбил Толя.
4.4. Проводник принадлежит к племени аборигенов.
4.5. И Косоглаз, и Борода являются жителями деревни Лгуново, Курнос — чередовец, Алощек — лгуновец, Длинноух — правдовец.
5.1. У Чернова волосы русые, у Белокурова — рыжие, у Рыжова — черные.
5.2. Толя живет в Москве, Витя — в СанктПетербурге, Юра — в Новгороде, Коля — в Перми, Алеша — в Томске.
5.3. Молоко находится в кувшине, квас — в банке, лимонад — в бутылке, вода — в стакане.
5.4. Алеша живет на улице Газон, учится в школе № 1 и любит математику.
Боря живет на улице Рогатица, учится в школе № 8 и любит биологию.
Володя живет на улице Ломоносова, учится в школе № 30 и любит химию.
5.5. Наташа вышла в синем платье и зеленых туфлях,
Валя — в зеленом платье и синих туфлях, Аня — в белом платье и белых туфлях.
5.6. Физик владеет французским и итальянским языками,
историк — русским и итальянским,
биолог — английским и французским,
математик — английским и итальянским.
6.1. Мальчики стояли в очереди в следующем порядке: Олег, Юра, Володя, Миша и Саша.
6.2. Места между командами распределились следующим образом:
на первом месте команда Д,
на втором — Е,
на третьем — Б,
на четвертом — В,
на пятом — Г,
на шестом — А.
6.3. Вере 5 лет, Боре 8 лет, Ане 13 лет, Гале 15 лет.
6.4. Юра Воробьев катался с Люсей Егоровой,
Андрей Егоров — с Олей Петровой,
Саша Петров — с Инной Крымовой,
Дима Крымов — с Аней Воробьевой.
6.5. У Гали платье зеленое, у Нади — розовое, у Вали — голубое, у Ани — белое.
6.6. Петя — брат Оли, и Петя танцевал с Леной;
Боря — брат Наташи, и Боря танцевал со Светланой;
Алеша — брат Светланы, и Алеша танцевал с Олей;
Коля — брат Лены, и Коля танцевал с Наташей.
6.7. Леня — сын Григория Аркадьевича, катался с Алексеем Ивановичем;
Андрей — сын Валентина Петровича, катался с Федором Семеновичем;
Тима — сын Алексея Ивановича, катался с Валентином Петровичем;
Коля — сын Федора Семеновича, катался с Григорием Аркадьевичем.
6.8. Мальчики с именами Альберт, Карл, Дидрих и Отто имеют соответственно фамилии: Дидрих, Альберт, Отто и Карл.
6.9. Коля влюблен в Галю, Галя — в Петю, Петя — в Таню, Таня — в Юру, Юра — в Зину и Зина — в Колю.
7.1. а) Начинающий выигрывает, если своим первым ходом берет один камень, а после хода противника, взявшего к камней, возьмет 4 — к камней.
Если в кучке 7 (или 8) камней, то выигрышная стратегия начинающего меняется незначительно: своим первым ходом он должен взять два (или три) камня.
б) Если в кучке 11 камней, то выигрышная стратегия для начинающего состоит в следующем: своим первым ходом он должен взять два камня, а затем после каждого хода противника, взявшего к камней, брать 4 – k камней.
7.2. Выигрышная стратегия начинающего состоит в том, что своим первым ходом он должен взять два камня, а потом после каждого хода противника, взявшего k камней, начинающий должен брать 4 – k камней.
Если начинающий допустил ошибку в своем первом ходе, то есть взял не два камня, а один (или три), то противнику следует взять один (или три) камня, и он получает в дальнейшем выигрышную стратегию начинающего.
Если начинающий допустил ошибку в своем втором (или последующем) ходе, то противник может получить выигрышную стратегию, поступив как и в случае задачи № 7.1.
7.3. а) Выигрывает начинающий, взяв своим первым ходом 14 камней, из кучки, содержащей 30 камней.
б) Выигрывает противник, пользуясь такой стратегией: если начинающий берет к камней из одной кучки, то противник должен взять также k камней, но из другой кучки.
7.4. Выигрывает противник, если после хода начинающего одной из пуговиц вперед на k клеток, он будет передвигать вторую пуговицу вперед также на k клеток.
7.5. Выигрывает начинающий, если он своим первым ходом передвинет одну из трех пуговиц на последнюю клетку, а далее будет пользоваться стратегией противника из задачи № 7.4.
7.6. Выигрывает начинающий, если он своим первым ходом ставит «крестик» (или «нолик») в центр доски.
7.7. Проигрывает начинающий. Выигрывает противник, если он будет ставить свои ладьи симметрично ладьям первого мальчика относительно центра доски.
7.8. Выигрышную стратегию в этой игре имеет начинающий, и состоит она в следующем: начинающий первым называет число 1, а в дальнейшем, после того как противник назовет число к. (не больше четырех), называет число (5 – k,) (i = 1, 2, 3, 4, 5).
7.9. Выигрышную стратегию имеет начинающий. Он первым называет число 1, а в дальнейшем, после того как противник назовет число k1. (не больше 10), называет число 11 – k(1 = 1, 2, …, 9).
8.1. А набрал 2,5 очка и разделил II–V места;
Б набрал 2,5 очка и разделил II–V места;
В набрал 2,5 очка и разделил II–V места;
Г набрал 2,5 очка и разделил II–V места;
Д набрал 2 очка и занял IV место;
Е набрал 3 очка и занял I место.
8.2. Решение задачи дается итоговой турнирной шахматной таблицей:
8.3. Решение задачи дается итоговой таблицей хоккейного турнира:
8.4. Решение задачи дается итоговой таблицей футбольного турнира:
8.5. Первый стрелок третьим выстрелом набрал 100 очков, а второй стрелок — 2 очка.
Илл.: С. Григорьев
ЛИТЕРАТУРА
- Кордемский Б. Спрятанная арифметика. — Квант, 1978, № 3.
- Цинман Л. Л. Логические задачи и алгебра высказываний. — Квант, 1971, № 4.
- Депман И. Я. Первое знакомство с математической логикой. — Л.: Общество «Знание», 1965.
- Лихтарников Л. М. Логические задачи. Элементы математической логики. — Л.: ЛГПИ им. А. И. Герцена, 1976.
- Лихтарников Л. М. Волшебное зеркало мага. — Квант, 1994, № 1.
6. Лихтарников Л. М. Задачи мудрецов. — М.: Просвещение
[1] В текст данной главы полностью включена статья автора, опубликованная в журнале «Квант» (1994, № 1) в разделе «,,Квант“ для младших школьников».

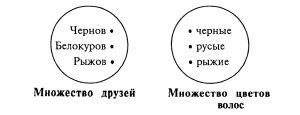
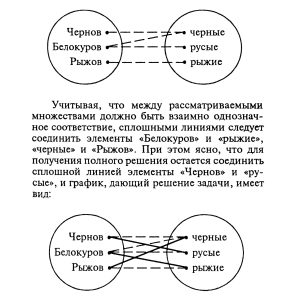
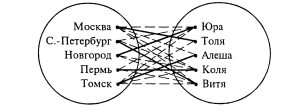
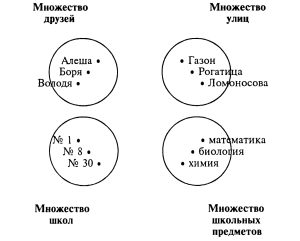
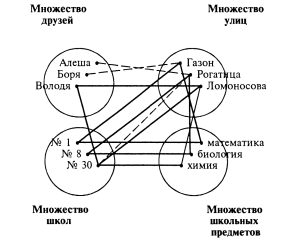
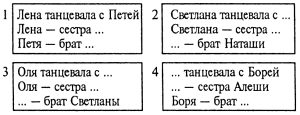

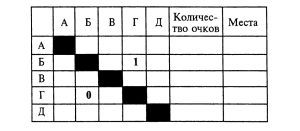
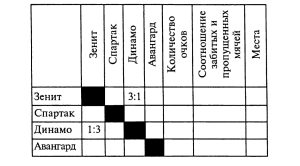
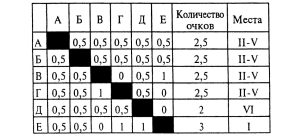
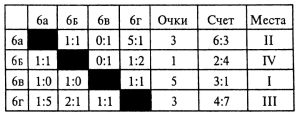
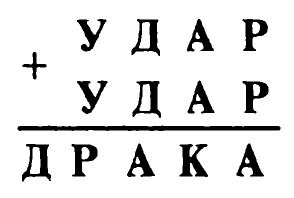
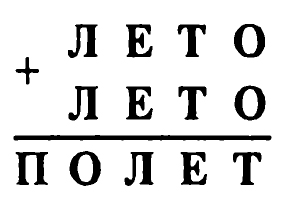
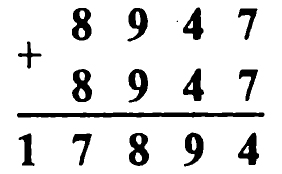
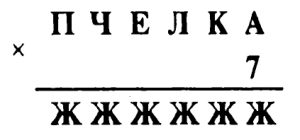
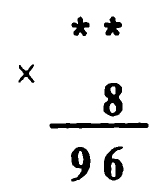
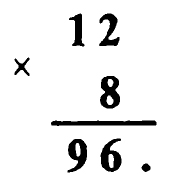
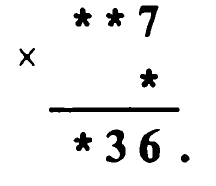
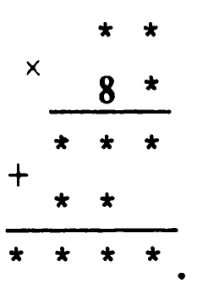
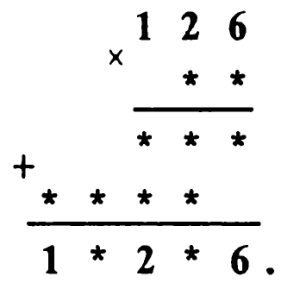
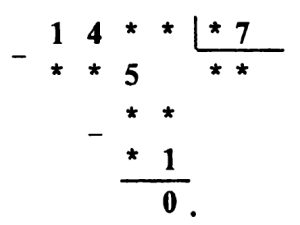
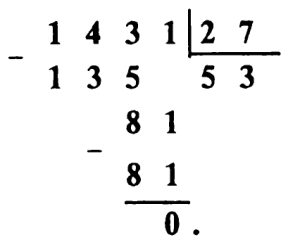
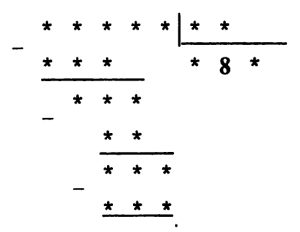
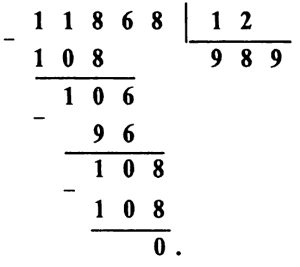
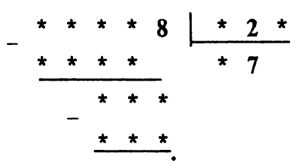
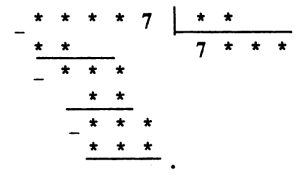
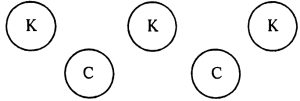
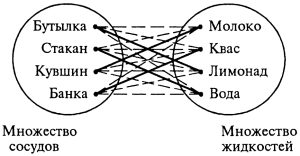
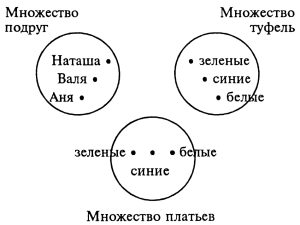
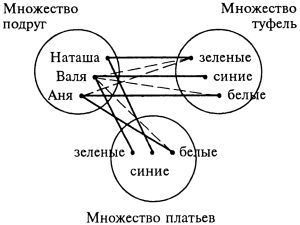
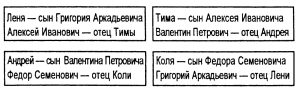
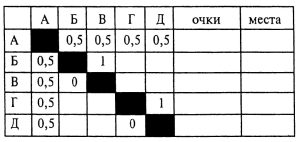
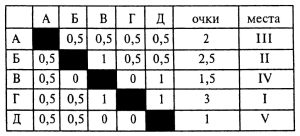


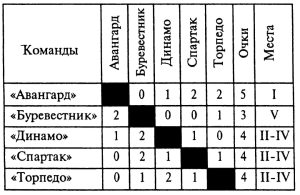

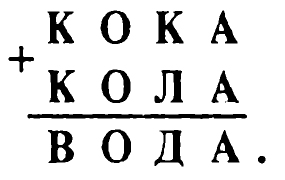
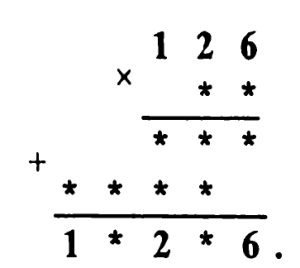
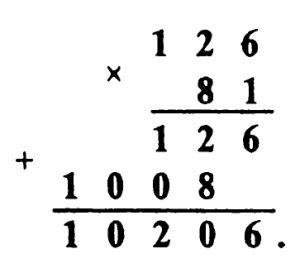
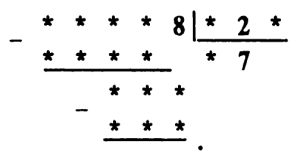
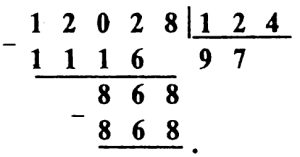
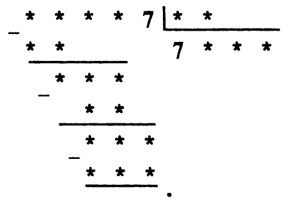
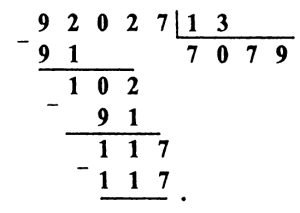
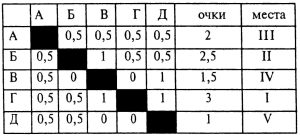
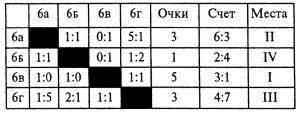
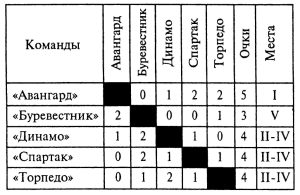


Комментировать