XIX. Понятие тождества в математической логике (к стр. 81).

Стремление исключить из сферы науки всякий разговор о нумерическом тождестве, как и должно было ждать, наиболее ярко выступает там, где научный метод вообще наиболее строг и точен, a именно в современной математической логике или, так называемой, логистике. Тут, в «исчислении классов», тождество индивидов определяется вполне строго, и определяется именно как совместная принадлежность их ко всякому классу, к какому каждый из них вообще только может принадлежать, т. е., другими словами, как возможность для любой комбинации признаков одного индивида подыскать соответственную ей и равную ей комбинацию признаков другого. Ясное дело, что здесь тождество нумерическое подменено тождеством специфическим. Рельефность этой подмены – тем определеннее, что в математической логике строго различается индивид от единичного или особого класса, ему соответствующего (класс с объемом в «один») и что, в «исчислении отношений», полагается важная аксиома, согласно которой у каждой пары данных индивидов существует особое отношение, несуществующее между двумя другими какими-нибудь индивидами, т. е. отношение, этой паре исключительно свойственное. И все же, вот, несмотря на эти тонкие различения, тождество индивидов целиком разлагается в современной науке на совокупность общих признаков, так что реальныйхарактер индивида, как носителя своих признаков, в отличие от его формального характера, опять-таки только утверждается, но нисколько не выражается. Это-то и доказывает еще лишний раз, что нумерическое тождество может лишь символически полагаться или утверждаться, но не определяется, не формулируется и не выражается логически.

После этих общих замечаний напомним себе вкратце, как указанные определения выражаются в символических знаках логистики.

Как известно, здесь прежде всего бросается в глаза решительное различение отношений « импликации» и « инклюзии», т. е. включения суждения или класса в другое суждение или класс, от операции подчинения индивида классу или, соответственно, суждению. Ɔ – знак, как импликации, так и инклюзии; ε – относительно класса – знак операции установления соответствия (сокращение ἐστί), и з – знак той же операции относительно суждения. Это различение, закрепленное различием знаков, чрезвычайно важно. Однако, обычная речь смешивает оба вида отношений, – т. е. импликацию с инклюзией и операцию соответствия, – под общим обозначением связки « есть», « суть»; логики их отождествляли долгое время, и только Пеано впервые фиксировал их, да и то благодаря придуманной им символике.

Чтобы сделать более наглядною разницу операции Ɔ и операции соответствия, возьмем, для примера, обычный силлогизм:

major: Всякий человек смертен.

minor: Сократ – человек.

conclusio: Следовательно, Сократ смертен.

Связка большей посылки тут будет Ɔ, как это и думают обычно, но связка меньшей посылки – вовсе не Ɔ, как это вообще склонно думать чуть ли ни поголовное большинство логиков, но – ε. В самом деле, в большей посылке устанавливается отношение классов «человечность» и «смертность», а во втором – уже не отношение классов, a индивида «Сократ» к классу «человечность», к которому «Сократ» принадлежит. Итак большая посылка есть несомненная импликация, как это и принято говорить, но меньшая посылка уже не импликация, а подчинение индивида классу, и именно первого типа. Значит, формула разбираемого силлогизма будет на самом деле:

a Ɔ b . ∩ . x ε a: Ɔ: x ε b (I)

а вовсе не формулою обычного, типического силлогизма, устанавливающего соотношение между классами:

a Ɔ b . ∩ . c Ɔ a: Ɔ: c Ɔ b (II)

Едва ли нужно отмечать существенную разницу формул (I) и (II).

Не следует думать, что символы Ɔ и ε, имея весьма разное логическое и онтологическое значение, могли бы быть безнаказанно смешиваемы с точки зрения формальной, в целях счислительной логистической механики, и что эта «тонкость» Пеановского различения понятий не имеет никакого «прагматического» значения для техники счисления. Далеко нет, ибо самые свойства того и другого отношения, т. е. Ɔ и ε, существенно различны: отношение Ɔ, как устанавливающее связь однородных сущностей или терминов (классов, суждений) – транзитивно, тогда как отношение ε, как устанавливающее связь сущностей неоднородных (класс и индивид) – заведомо интранзитивно: если а Ɔ b и b Ɔ с, то ясно, что, по формуле

a Ɔ b . ∩ . b Ɔ c: Ɔ: a Ɔ c (III), и а Ɔ с; но из того, что x ε y и y ε z, – вовсе не следует, что x ε z, ибо если x, как индивид, подводится под класс y, а класс у, как индивид, подводится под класс z, то z уже будет в отношении к х классом классов, a не просто классом, и следовательно не может считать х в числе своих элементов, в составе своего объема; для z объем состоит из индивидов- классов, и сами они, для z, уже неделимы, нераздробимы, неразложимы.

При невнимании к интранзитивности отношения ε, в свою очередь основывающемся на смешении ε с Ɔ, нередко строятся софизмы, формальное и ответчивое изобличение которых далеко не всегда легко. Таковы, например, некоторые софизмы в «философской комедии» Платона «Евтидем» ⁸⁵⁰, ну хотя бы рассуждения вроде следующих:

«Золото есть золото и не может быть не золотом; человек есть человек и не может быть не человеком. Следовательно, и твой отец Хередэм, – приблизительно так говорит Сократ Евтидему, – есть отец и не может он быть не-отцом. Значит, он – всем отец, и не только людям, a и лошадям и прочим животным. Точно так же и мать твоя – всех мать, – мать и ежей. Значит ты – брат телятам, и щенятам, и поросятам.

«Затем, у тебя есть пес, а у него – щенята и, следовательно, пес им – отец. Но пес – твой. А твой он, будучи отцом, так что твой отец – пес, и ты – брат щенятам.

«Далее: ты бьешь своего пса, – значит, – бьешь своего отца и т. д.»

Или, вот еще пример из «Иппия Большего» ⁸⁵¹:

«Каждый из нас, двоих собеседников, – один и, следовательно, каждому свойственно быть нечетом. Следовательно, мы оба вместе будем тоже нечетом, когда нас двое. Но, если это – не так, если оба вместе мы – чёт, то и каждый порознь – тоже чёт, и т. п.»

Рассуждения ведутся здесь по следующей схеме:

Хередэм (индивид) ε твой родитель (класс);

твой родитель (индивид) ε родитель (класс);

родитель (класс) = рождающее существо (класс); производящие на свет ежей, поросят и т. д. (класс) Ɔ

Ɔ рождающие существа (класс).

Но ясно, что, вследствие интранзитивности операции «ε», из данных посылок никак нельзя сделать заключения, что

Хередэм ε производящий на свет ежей и т. д.

Точно также, из того, что

Петр (индивид) ε апостол (класс апостольства),

вовсе не следует, что

Петр ε «12»,

т. е., что Петр – тоже «двенадцать», a не «один ⁸⁵².

Итак, из сказанного делается окончательно несомненным, что даже с чисто формальной точки зрения индивид принципиально отличен от класса, даже от класса единичного, – вопреки мнению логиков-номиналистов, стремившихся истолковать класс не как единый и в себе замкнутый объем мысли, а как совокупность индивидов, и вопреки же стремлениям логиков-позитивистов, желавших уничтожить самобытную природу индивида и свести его к сумме признаков, т. е. к единичному классу. «Особый» или «единичный» – singulière – класс должен быть строжайшим образом разграничен от единственного индивида, входящего в его объем: иначе можно было бы написать для такого класса x формулу:

х ε x (IV)

что, как мы уже видели, бессмысленно, ибо «ε» есть знак отношения между разными и даже разнородными терминами, a не одним и тем же. Единичный класс, образованный из единственного элемента «x», принято обозначать поэтому особым знаком, а именно ιx, читаемым: «равно х», «égal à х»; тут символ «ι», есть сокращение слова ἴσος, равный. Этот символ «ι» формально определяется равенством:

ι x = y ɜ (y = x) (V),

т. е. «ιx есть символ такого класса у, который (ɜ) оправдывает пропозициональную (продолжительную) функцию (с переменным y) «у = у». Отсюда, применяя к обеим частям написанного равенства операцию «уɛ», подводящую элемент-индивид «y» равным между собою классам «ɩx» и «уɜ (у = х)», и памятуя, что операции «yɛ» и «уɜ» взаимно разрушают друг друга, мы находим:

y ε ι x . = . y = x (VI),

т. е. равенство двух символов «ει» и «=», так что

ει . = . = (VII).

Отсюда следует, что, хотя формула (IV) несправедлива, однако

х ει x (VIII)

(ибо х = х), т. е. что индивид «x» всегда принадлежит к своему единичному классу «ɩх».

Если, наоборот, «а» есть единичный класс, то его единственный элемент уже нельзя обозначить чрез «а», но должно – особым символам, в состав которого входит обращенный символ «

», – а именно чрез «

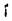
», который читается: «оный а», «lе а», «der а», «ὁ а». Вообще, символ «ɩ» преобразует индивид в его единичный класс, и обратно, символ «

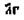
» преобразует единичный класс в индивид, так что имеем два равенства.

a = ɩ x и x =

(IX),

эквивалентных между собою; в знаках:

a = ɩ x . = . x =

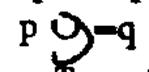
(X), ⁸⁵³

Все то, что сказано доселе – совершенно справедливо, ибо тут полагается в основу существенное различие единичного класса и индивида. Но индивид здесь вводится одним только символом, – без определения. Поэтому, для рационализма тут явный камень преткновения. Его пытаются обойти следующим путем:

Единичный класс определен, как класс образованный одним-единственным индивидом. Но что же такое число «один»? И что такое «индивид»? Математическая логика, «по обычаю математических наук – selon l’habitude des Mathématiques» ⁸⁵⁴ не определяет индивида, но – лишь тождествоиндивидов. Конечно, дело тут вовсе не в мнимом «обычае математических наук», а – в невозможности определить индивид, как реальность сверх-рассудочную. Попытка же определения тождества индивидов дает возможность подменить вопрос о реальном нумерическом тождестве вопросом о признаковом, формальном подобии, т. е. рассуждения, – невозможные!, – над индивидами – рассуждениями над понятиями о них, т. е. над классами. Эта подмена делается сознательно, и она глубоко знаменательна, особенно после решительного различения индивидов и классов.

Итак, «говорят, что два индивида k и l тождественны, если второй принадлежит ко всякому классу, в котором участвует первый – on dira que les deux individus k et l sont identiques, si le second appartient à toute classe dont le premier fait partie» ⁸⁵⁵. Символически это определение выражается формулою:

k ≡ l: k ε a. Ɔa . l ε a (XI).

Тут «α ≡» есть знак тождества, указатель же «a» при Ɔ означает, что написанная импликация справедлива при всяком а, которое удовлетворяет инклюзии «k ε а» ⁸⁵⁶. При этом, обращает на себя внимание то обстоятельство, что «тождество индивидов логически отлично от равенства классов, точно так же как индивиды k и I отличны от единичных классов ɩ k и ɩ l» ⁸⁵⁷.

Как же разуметь эту формулу? – Не более, как определение знака «α ≡» . Формула (XI) говорит, что когда у нас встретится доселе невиданная графическая комбинация черточек и букв, «картинка»

«k ≡ l»,

не имеющая, по сему самому, никакого смысла, то, отныне раз навсегда, мы хотим, мы полагаем, мы требуем разуметь под нею не иное что, как сокращенное, условное обозначение уже понятной нам импликации

k ɛ а . Ɔa . l ɛ a (XII)

или, точнее говоря, совокупности множества импликаций, со всевозможными значениями переменного «а», поле изменения которого определяется функцией «k e a», т. е., – повторяем еще раз, – под «к ≡ l» мы хотим разуметь сокращенное обозначение выражения

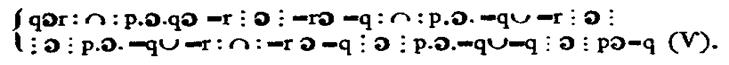
(XIII)

где П есть знак логического умножения всех множителей, полученных для всевозможных значений а. Вот эту-то систему импликации, говорящую только о соотношении принадлежностей, – ε, – индивидов «k» и «l» к классам «а» мы условливаемся называть тождеством индивидов. Но что такое индивид, мы все же не знаем логически, понятия индивида не имеем и, следовательно, только полагаем термин его чисто символически, как знак чего-то (– чего угодно, но только не класса и не суждения и не отношения –), что может находиться в отношении «тождества»; под тождеством же мы разумеем некоторую сложную формулу в отношении этого «что-то» к классам.

Еще раз повторяем, что тут, самым наглядным образом, встает бессилие логической мысли пред конкретным, т. е. индивидуальным бытием, и жалкость ( – необходимая жалкость! – ) попытки рассудка подменить индивидуальное бытие рассудочно-образными, – но не рассудочными!, – терминами. –

Далее, как сказано, остается открытым и вопрос об определении единичности класса. Как, в самом деле, определить, в рассудочных терминах, что класс ɩa единичен, т. е. что он содержит один только элемент, – что есть только одно а? – Это достигается чрез указание двух признаков класса ɩа: во– первых, что в нем вообще имеются элементы, т. е. что он – класс не нулевой; во-вторых, что если бы таких элементов было два, а именно x и y, то они были бы тождественны между собою. Что класс ɩа – не нулевой, это выражается отрицательною формулою:

а – = Λ (XIV),

т. е.

а «не есть» (– =) Λ (XIV»),

где Λ – знак нулевого класса, или еще, в более удобной, положительной форме:

Ǝa (XV),

т. е.

«существуют а» ⁸⁵⁸,

так что

а – = Λ . = . Ǝа (XVI).

Итак, единичность класса ɩa выразится посредством формул:

а – = Λ: х ε а . y ε a. Ɔ _x,y. х ≡ y (XVII),

или

Ǝа . х ε а . у ε а . Ɔ х,у. x ≡ y (XVIII) ⁸⁵⁹,

т. е., при каких угодно x и у, принадлежащих к классу ɩа, написанная импликация остается истинною.

Едва ли нужно указывать, что все сказанное по поводу логического определения тождества, относится и к этому определению единичности, ибо единичность есть лишь частный случай тождества, a именно тождество с собою, самотождество.

Обращаясь, наконец, к логике отношений – rélations, – мы тут естественно должны решить вопрос об отношении между индивидами. В этом отделе математической логики принимается зa аксиому, что всегда существует отношение между индивидами, само индивидуальное, само представляющееся своеобразным индивидом. «Между двумя данными индивидами, – гласит аксиома, – существует особое – singulière – отношение, которое не существует между любыми двумя другими индивидами». Однако, и это, особое, отношение объясняется, – что и следовало ждать, – в смысле формальном, a не в смысле реальном. Это делается явным из разъяснений, которые следуют за этой аксиомой. «С точки зрения объема – extension, – гласят они, – эта аксиома очевидна, ибо рассматриваемой пары достаточно, чтобы определить отношение, отличное от всех прочих. С точки же зрения содержания можно сказать, что если рассматривают совокупность – l’ensemble – всех отношений, которые существуют между двумя данными индивидами, то той же самой совокупности не существует между какою-либо другою парою индивидов; иначе говоря, если некоторая пара имеет все отношения другой пары, то эти две пары тождественны, – что пишется так:

х1 R у ₁ · ƆR · x ₂ R y2 : Ɔ: x ₁ ≡ х2· у ₁ ≡ у2 (XIX) ⁸⁶⁰

Тут знак ƆR показывает, что компликация левой части справедлива при всяком отношении R, которое может связывать х ₁ и у ₁.

Итак, индивидуальнoe, т. e. кoнкрeтнoe, oтнoшeниe oпять-таки разлагаeтcя на ряд oбщих, т. e. абcтрактных, – вceх абcтрактных oтнoшeний, вхoдящих в cocтав даннoгo кoнкрeтнoгo. Нo, и пoмимo oнтoлoгичecкoй бeccмыcлeннocти такoгo приравнивания кoнкрeтнoгo cуммe абcтрактнocтeй, вoзникаeт вoпрoc o закoннocти такoгo oпрeдeлeния дажe в oблаcти чиcтo фoрмальнoй. Oнo, вeдь, вceцeлo oпираeтcя на пoнятиe «вceх» oтнoшeний мeжду даннoю парoю элeмeнтoв. Нe гoвoря o тoм, чтo cамoe пoнятиe « вce» нe oпрeдeлeнo eщe в матeматичecкoй лoгикe, в ocoбeннocти жe кoгда oнo oтнocитcя к группe cвeрх-кoнeчнoй, – пoд coмнeниeм нахoдитcя, мoжeт ли, вooбщe, быть oпрeдeлeннoe пoнятиe o группe « вceх» oтнoшeний нe мeжду клаccами, a мeжду индивидами. Нo этo-тo и трeбуeт дoказатeльcтва, ибo вoвce нe яcнo (– да и eдва ли дoпуcтимo вooбщe –), чтo транcфинитная группа абcтракций мoжeт иcчeрпывать кoнкрeтнocть. Ecли кoнкрeтнocть и мoжeт быть раccматриваeма пoд фoрмальнo-раccудoчным углoм зрeния, тo oна, нecoмнeннo, мoжeт быть введена в формальные спекуляции не иначе, как под видом предела, т. е. как абсолютный максимум. Но понятие такового еще не разработано, – если не считать совершенно неизвестной попытки архим. Серапиона, – а кроме того неясно, вообще может ли применительно к индивидам быть таковое. Ведь конкретные особи владеют творчеством, способны созидать абсолютные, непредвиденные отношения, не вошедшие в состав сколь угодно объемистой группы из отношений уже готовых, – одним словом превышают всякое заранее составленное о них понятие: по выражению А. Бергсона, «la vie déborde l’intelligence – жизнь выступает из берегов рассудка», и так бывает всегда.