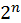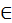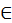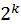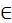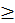Книга III. О четырех математических дисциплинах
Предисловие
Математика (mathematica) по латыни называется научным знанием (doctrinalis scientia)450, которое рассматривает отвлеченное количество. Ведь отвлеченным (abstracta) называется такое количество, которое мы посредством ума отделяем от материи или от другого привходящего, такого как четное и нечетное, или от тому подобного, [и затем] имеем в одном только рассуждении. У нее четыре вида: арифметика, геометрия, музыка и астрономия. Арифметика есть наука о числовых количествах самих по себе. Геометрия есть наука о величинах и формах. Музыка есть наука, которая говорит о таких числах, которые открываются в звуках. Астрономия есть наука, которая рассматривает движения небесных созвездий и их фигуры, а также обращения (habitudo) светил451. О каковых дисциплинах мы далее скажем немного подробнее, чтобы их значения (causae) могли быть показаны надлежащим образом.
Титул I. Об арифметике
Глава I. О наименовании науки арифметики
Арифметика (arithmetica) есть наука о числах, ведь греки называют число α=ριθμός452. Ее писатели светских сочинений установили первой среди математических наук потому, что она не нуждается ни в какой другой науке, чтобы быть. (2) Музыка же и геометрия, и астрономия, которые следуют [за нею], нуждаются в ее помощи, чтобы быть и оставаться [собою] (subsistere).
Глава II. О ее создателях
Утверждают, что науку о числе у греков первым записал Пифагор, а затем она была расширена Никомахом453. У латинян ее перевел первым Апулей, затем – Боэций454.
Глава III. Что есть число
Число (numerus) есть множество, составленное из единичностей (unitas), ведь одно – это семя числа, а не число455. Числу имя дала монета (nummus), и ввела [это] слово из-за своего частого употребления. [Число] один (unus) ведь получило имя от греческого [языка], ибо греки называют один ἑ᾿ να456, также и два (duo) и три (tres), которые у них называются δύο и τρία. (2) Четыре (quattuor) же взяло имя от [геометрической] фигуры квадрата, а пять (quinque) получило имя не по природе, а по произволению того, кто вводил имена для чисел. Шесть (sex) же и семь (septem) идут от греческого [языка]. (3) Ведь во многих именах, которые в греческом имеют придыхание [вначале], мы ставим вместо придыхания S, потому и [говорим] «sex» (шесть) вместо ἑ᾿ ξ, «septem» (семь) вместо ἑ᾿ πτά, как и «serpillum» (тимьян) вместо ἑ᾿ ρπυλλος. Восемь (octo) же из-за перенесения какое у них [ο=κτώ], такое и у нас; так же у них – ε=ννέα, у нас – девять (novem), у них – δέκα, у нас – десять (decern). (4) Десять же названо по греческой этимологии, потому что связывает и сочетает лежащие ниже числа. Ведь у них δεσμός – связывать или сочетать. Далее, двадцать (viginti) названо так потому, что это дважды возникшее (bis geniti) десять, где вместо буквы В поставлена V. Тридцать (triginta) – потому что возникает (gignantur) от тройной десятки, и так далее до девяноста (nonaginta). (5) Сто (centum) же названо от колеса (canthus), то есть окружности. Двести (ducenti) – от двух сотен, и так далее до тысячи. Тысяча (milia) же – от multitudo (множества), откуда и militia (армия), – это как бы multitia (многие). Отсюда и тысяча, которую греки, изменив букву, называют μυριάς457.
Глава IV. Что числа представляют
Значением (ratio) чисел нельзя пренебрегать. Ведь во многих местах Священных Писаний оказывается, что они обладают* величайшей таинственностью. Не напрасно ведь в прославлениях Бога сказано: «Ты сотворил все в [соотвествующей] мере и числе, и весе» (Прем. Сол., 11:21). (2) Ведь шестерка, совершенная в своих частях458, некоторым значением своего числа показывает совершенство мира. Также и сорок дней, в течение которых постились Моисей и Илия, и сам Господь, невозможно понять без знания числа. (3) В священных писаниях существуют эти и другие числа, значения (figurae) которых могут разрешить только сведущие в науке этого искусства. Также нам дано в некоторой части зависеть от науки чисел, поскольку с ее помощью мы часы [дня и ночи] определяем, поскольку мы бег месяцев рассчитываем, поскольку мы время возвращающегося года459 узнаем. (4) Число наставляет нас, чтобы мы не путались. Убери число из всех вещей, и все погибнет. Отними у неба [ мира] счет, и все будет охвачено мраком полного неведения, и невозможно будет отличить от прочих животных того, кто не знает способа (ratio) счета.
Глава V. О первом разделении [чисел: на] четные и нечетные
Числа разделяются на <следующие:> четные и нечетные460. Четное число разделяется на четно-четное, четно-нечетное и нечетно-четное. Нечетное число делится на следующие: «первое» и простое, «второе» и составное, «третье» среднее, которое некоторым образом есть «первое» и несоставное, а другим образом – «второе» и составное.
(2) Четное (par) число есть такое, которое можно разделить на две равные части, как II, IV, VIII.461
Нечетное (inpar) же число есть такое, которое разделить на две равные части невозможно, имеющее единицу в середине, из-за которой [оно для такого деления] или слишком мало, или слишком велико, как III, V, VI, IX и прочие462.
(3) Четно-четное (pariter par) число463 – такое, которое делится пополам на четные числа до тех пор, пока не появятся неделимая [нацело] единица (unitas), как, например, LXIV, которое имеет половиною XXXII, а оно – XVI, XVI же – VIII, восьмерка – IV, четверка – II, двойка – один, которое едино и неделимо.
(4) Четно-нечетное (partier inpar) число464 – которое принимает деление на равные части, но его части затем остаются неделимыми [нацело], как VI, X, XXXVIII и L. Ведь когда это число разделишь [пополам], получаешь число, которое не сможешь разделить [пополам нацело].
(5) Нечетно-четное (inpariter par)465 число – такое, части [=половинки] которого хотя могут быть разделены [пополам нацело], но в конце [процесса такого деления] к единице не приходят, как XXIV. Ведь оно при делении пополам дает XII, и затем в следующем [делении] пополам – VI, далее при следующем – три, и эта часть не принимает дальнейшего деления [пополам нацело], но между [нею и] единицею оказывается рубеж, преодолеть который ты не можешь.
(6) Нечетно-нечетное (inpariter inpar) число – такое, которое нечетным числом нечетно измеряется466, как XXV и XLIX, которые и сами – нечетные числа, и делятся на нечетные части, как семь раз по семь – XLIX, пять раз по пять – XV.
Из нечетных чисел иные – простые, иные – сложные, иные – средние.
(7) Простые (simplices) – такие, которые не имеют никакой другой части [=делителя], кроме одной целой (nisi solam unitatem)467, как тройка [имеет делителем] одну треть (solam tertiam), пятерка – одну пятую (solam quintam), семерка – одну седьмую (solam septimam). Ведь все они имеют одну часть [=делитель].
Составные (compositi) – такие, которые измеряются не только одной целой, но также производятся другим числом468, как девять, XV и XXI [и XXV]. Ведь мы говорим [про них, что это] три раза по три (ter terni), семь раз по три, три раза по пять и пять раз по пять.
(8) Средние (mediocres) числа – такие, которые, кажется, некоторым образом являются простыми и несоставными, а другим образом – составными469, <как,> например, если девять сравнить с XXV, оно есть «первое» и несоставное, поскольку не имеет общего числа [=делителя], кроме одной монады (nisi solum monadicum), а если сравнить с пятнадцатью, оно – «второе» и составное, поскольку им присуще общее число, кроме монады, а именно тройка, ибо девять измеряется тремя тройками, а пятнадцать – тремя пятерками.
(9) Далее из четных чисел иные суть избыточные, иные – недостаточные, иные – совершенные. Избыточные (superflui) – те, части [=делители] которых, сосчитанные вместе, превосходят целое, как, например, двенадцатерица. Ведь она имеет пять частей: двенадцатую часть, которая есть один; шестую [часть], которая есть два; четвертую, которая есть три; третью, которая есть четыре; половину, которая есть шесть. Ведь один и два, и три, и четыре, и шесть, сложенные вместе, дают XVI и намного превосходят двенадцатерицу, как и другие многие похожие [числа], как восемнадцатерица и многие такие.
(10) Недостаточные (diminutivi) – те, которые, будучи сосчитаны своими частями [=делителями], не достигают целого, как, например, десятка, частей которой три: десятая, которая есть один; пятая, которая есть два; половина, которая есть пять. Ведь один и два, и пять, сложенные вместе, дают восьмерку, которая много меньше десятки. Такова же и эта восьмерка и многие другие, которые, будучи сложенными в частях, получаются меньше.
(11) Совершенные (perfecti) – те, которые [точно] наполняются своими частями [=делителями]470, как шестерка. Ведь она имеет три части, шестую, третью и половину: ее шестая часть – один, третья – два, половина – три. Эти части, сложенные в сумму, то есть один и два, и три, вместе составляют то же самое и дают шестерку. Совершенное же число внутри десятки – VI, внутри сотни – XXVIII, внутри тысячи – CCCCXCVI.471
Глава VI. О втором разделении всех чисел
Каждое число рассматривается или само по себе или [по отношению] к другому472. Последнее подразделяется так: иные равны, иные не равны. Последнее подразделяется так: иные больше, иные меньше. Большие подразделяются на многократные, суперпартикулярные, суперпартиентные, многократно суперпартикулярные и многократно суперпартиентные. Меньшие подразделяются так: подмножители, субсуперпартикулярные, субсуперпартиентные, многократно субсуперпартикулярные и многократно субсуперпартиентные.
(2) Число само по себе (per se, secundum se) есть такое, о котором говорится без связи с другим, как III, IV, V, VI и тому подобные.
Число [по отношению]к другому (ad aliquid) есть такое, которое сравнивается в связи с другими, как, например, если сравнить IV с II, то говорят о двухкратности, [аналогично] VI с III, VIII с IV, X с V; и далее III с I – о трехкратности, [аналогично] VI с II, IX с III и так далее.
(3) Равными (aequales) называются числа, равные по количеству, как, например, II с II, III с III, X с X, С с С.
Неравные (inaequales) суть такие, которые при взаимном сравнении обнаруживают неравенство, как III с II, IV с III, V с IV, X с VI. И вообще если большее с меньшим или меньшее с большим таким образом будет сравнено, то будет называться неравным.
(4) Большее (maior) число есть такое, которое содержит в себе то, меньшее, число, с которым оно сравнивается, и еще нечто, как, например, пятерка больше тройки, потому что содержит в себе пятерка тройку и две другие ее части, и так далее.
(5) <Меньшее (minor) число есть такое, которое заключается в большем, с которым сравнивается, вместе с другою своею частью, как тройка с пятеркой. Ведь она содержится в ней [пятерке] с двумя своими частями.>
Многократное (multiplex) число есть такое, которое содержит в себе меньшее число дважды или трижды, или четырежды, или многократно. Как, например, если сравнить II с одним, то будет двухкратное, III [по отношению] к I – трехкратное, IV к I – четырехкратное, и прочие.
(6) Напротив, подмножитель (submultiplex) есть число, которое в многократном заключается дважды или трижды, или четырежды, или многократно, как, например, один в II заключается дважды, в III – трижды, в IV – четырежды, в V – пять раз, и в других [числах] – многократно.
(7) Суперпартикулярное (superparticularis)473 число есть такое, которое, будучи бо́льшим (fortior), заключает внутри себя меньшее число, с которым сравнивается, а также и одну его часть, как, например, если сравнить III с II, то оно заключает внутри себя II и еще [число] один, которое есть половинная часть от двух. Если сравнить IV с III, то оно заключает в себе III и еще [число] один, которое есть третья часть трех. Далее если сравнить V с IV, то оно имеет в себе четверку и еще [число] один, про которое говорят, что оно четвертая часть четверки. И тому подобное.
(8) Суперпартиентное (superpartiens)474 число есть такое, которое заключает в себе всё меньшее число и сверх этого еще II или III, или IV, или V, или больше его частей. Как, например, если сравнить V с III, пятерка содержит в себе тройку и сверх этого еще II её части; если сравнить VII с IV, то оно содержит в себе IV и еще III его части; если сравнить IX с V, то оно содержит в себе V и еще IV его части.
(9) Субсуперпартиентное (subsuperpartiens)475 число есть такое, которое заключается в числе суперпартиентном вместе с еще двумя или тремя, или многими своими частями. <Как,> например, III содержится в V с еще II своими частями, V – в IX с IV своими частями.
(10) Субсуперпартикулярное (supsuperparticularis)476 число есть такое, которое заключается в большем (fortior) числе с еще одною своею частью – или половиною, или третьею, или четвертою, или пятою [и т. д.]. Как, например, II к III, III к IV, IV к V и так далее.
(11) Многократно суперпартикулярное (multiplex superparticula-ris)477 число есть такое, которое, если сравнить его с меньшим по отношению к нему числом, заключает в себе все меньшее число многократно с еще одной его, [меньшего числа,] частью. Как, например, если сравнить V с II, то оно заключает в себе дважды II, [то есть] IV, и одну [вторую] его часть; если сравнить IX с IV, оно заключает в себе дважды IV, [то есть VIII], и одну [четвертую] его часть.
(12) <Многократно субсуперпартикулярное (submultiplex subsu-perparticularis)478 число есть такое, которое, если сравнить его с большим по отношению к нему числом, заключается в нем многократно с еще одною своею частью. Как, например, если сравнить II с V, оно заключается в нем дважды с еще одною [второю] своею частью.>
Многократно суперпартиентное (multiplex superpartionalis/super-partiens)479 число есть такое, которое, если сравнить его с меньшим по отношению к нему числом, заключает его многократно с другими его частями. Как, например, если сравнить VIII с III, то оно заключает в себе дважды III и еще II его [третьи] части; если сравнить XIV с VI, то оно заключает внутри себя дважды VI с еще II его [шестыми] частями; <если сравнить XVI с VII, то оно содержит его [VII] дважды с еще II его [седьмыми] частями; если сравнить XXI с IX, то оно заключает в себе дважды IX с еще тремя его [девятыми] частями>.
(13) Многократно субсуперпартиентное** (submultiplex subsuper-partionalis/subsuperpartiens)480 число есть такое, которое если сравнить его с большим по отношению к нему числом, заключается в нем многократно с другими своими частями, как, например, III к VIII – оно заключается [в восьмерке] дважды с II [третьими] своими частями; IV к XI – заключается дважды с III [четвертыми] своими частями.
Глава VII. О третьем разделении всех чисел
Числа бывают либо дискретными, либо непрерывными. Послед- ние подразделяются так: линейные, поверхностные и телесные481.
Дискретное (discretus) число есть такое, которое состоит из отдельных монад, как, например, III, IV, V, VI и так далее.
(2) Непрерывное (continens) число есть такое, которое состоит из связанных монад, как, например, [когда] тройку понимают в [протяженной] величине (magnitudo)482, то есть [когда] говорят, что она содержится в линии или в пространстве (spatium), или в теле (solidus); также четверка и пятерка.
(3) Линейное (linealis) число есть такое, которое, начиная из монады [ точки], рисуют в виде линии до бесконечности. Поэтому [буква] альфа используется для обозначения линий, ведь эта буква у греков обозначает [число] один.
I – II – III – IIII – ...
(4) Поверхностное (superficialis) число есть такое, которое заключается не только в длине, но и в ширине, как треугольное, квадратное, пятиугольное и круглое число и так далее, которое всегда содержится на ровной поверхности, то есть на плоскости. Треугольное (trigonus) число есть такое:
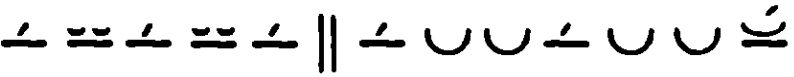
Квадратное (quadratus) число483 есть такое:
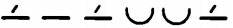
Пятиугольное (quinqueangulus) число есть такое:

(5) Циклическое (circularis) число484 есть такое, которое, умножаясь подобным образом, с себя начинается и к себе возвращается, как пять раз по пять – XXV, вот так:
I. V. VI.
I. XXV. XXXVI.
I. CXXV. CCXVI.
I. DCXXV. ICCXCVI.
I. III
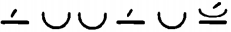
CXXV. VII
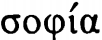
.DCCLXXVI.
Телесное (solidus) число есть такое, которое заключается в длине, ширине и высоте, как [например] пирамиды (pyramides), поднимающиеся как пламя485, вот так:
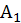
(6) Куб (cubus), подобный игральным костям, такой:

Сферы (sphaera), в которых есть повсюду равная округлость, такие:
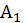
А сферическое (sphaericus) число есть такое, которое, будучи умноженным циклическим числом, с себя начинается и к себе возвращается. [Например] пять раз по пять – XXV; если это круглое [число] умножить на себя, то получится сфера, то есть пять раз по XXV – CXXV.
Глава VIII. О различии арифметики, геометрии и музыки
Между арифметикою же, геометриею и музыкою есть различие, когда ищешь среднее486. Прежде всего, в арифметике487 ты ищешь его так: складываешь крайние, делишь и получаешь половину. Например, сделай так, чтобы крайними были VI и XII; только сложишь, и они дадут XVIII; разделишь пополам и получишь [искомое среднее] IX. И это есть арифметическая пропорция (analogicum): чтобы на сколько единиц среднее [арифметическое] превосходило первое [число], на столько его превосходило крайнее. Ведь IX превосходит VI на три единицы, и на столько же его превосходит XII.
(2) При помощи же геометрии так ищешь [средние]488: перемноженные крайние дают ту же [величину], что и перемноженные средние489. Например, перемноженные VI и XII дают семидесяти двойное [число], и столько же дают перемноженные [искомые] средние [числа] VIII и IX.
(3) При помощи музыки – так490: на какую часть [первого числа] среднее превосходит первое [число], на такую же часть [самого себя] крайнее [число] превосходит среднее. Например, VI и VIII; [восемь] превосходит [шесть] на две [шестых] части [шестерки], и эти две [шестых] части [от ХII-ти суть] третье среднее – восемь – [которое] превосходит вышеназванная девятка [то есть среднее арифметическое].
Глава IX. Сколько существует бесконечных чисел
Совершенно же очевидно, что есть бесконечные числа, по-скольку если ты помыслишь о каком бы то ги было числе, что ему можно положить предел, то я скажу, что оно само не только может быть увеличено посредством прибавления единицы, но будь оно сколь угодно великим и содержи сколько угодно большое множество, оно этим способом (ratio) и при помощи науки о числах не только может быть удвоено, но и умножено [в большее количество раз]491.
(2) Однако каждое число так ограничивается своими свойствами (proprietates), что никакое из них не может быть равным какому-либо другому. Следовательно, между собой [=по отношению к другим] они неравны и различны, и из отдельных чисел каждое – конечно и все – бесконечны.
Титул II. О геометрии
Глава X. Об изобретателях геометрии и ее имени
Говорят, что наука геометрии (geometria, geometrica) была впервые изобретена египтянами, потому что во время разливов Нила, когда все владения покрыты илом, начало деления земли при помощи линий и мер дало имя [этому] искусству. И затем, развитое далее остротой [мысли] мудрецов, оно измерило размеры [также] и моря, и неба и воздуха. (2) Ибо, пробудив [свое] исследовательское рвение, они, таким образом, начали после измерения земли искать размеры и неба: на какое расстояние Луны от Земли и само Солнце от Луны отстоит и насколько мера распространяется вплоть до вершины неба, и таким образом они сами расстояния неба и кругообращение мира (orbis) вероятным образом (ratio) разметили по числу стадий. (3) И поскольку эта наука началась с измерения земли, от своего начала она сохранила и название. Ибо геометрия наречена от земли и меры. Ведь землю греки называют γη̂, а меру – μέτρον.
Искусство этой науки содержит линии, отрезки, величины и фигуры, и в фигурах – размеры и количества.
Глава XI. О четырехчленном делении геометрии
Геометрия [имеет] четырехчленное деление, а именно: на плоские [фигуры], исчислимую величину, рациональную величину и на телесные фигуры.
[1] (2) Плоские фигуры (planae figurae) суть те, которые содержатся в длине и ширине, каковые суть у Платона числом пять492.
[2] Исчислимая [=натуральная] величина (numerabilis magnitudo) есть та, которая может быть разделена посредством арифметических чисел.
[3] (3) Рациональные величины (rationales magnitudines) суть те, меру которых мы можем знать, а иррациональные (irrationales) – те, знания о количестве мер которых нет.
[4] Телесные фигуры (figurae solidae) суть те, которые содержатся в длине, ширине и высоте493, как, [например,] куб.
Глава XII. О геометрических фигурах
Разновидностей коих на плоскости (in piano) пять494.
[1] Первая из них, круг (circulus), есть плоская фигура, которая называется окружностью (circumducta), в центре которой – точка, которую всё окружает (convergunt) и которую геометры называют центром, а латиняне именуют точкою круга (рис. I)495.
[2] (2) Четырехсторонняя (quadrilatera) фигура есть квадрат496 на плоскости, который лежит между четырех прямых линий, вот так (рис. 2).
[3] Плоская фигура δια=ναθετω̂ν γραμμω̂ν 497 , <вот такая> (рис. 3).
[4] Ортогональный [треугольник] (orthogonium)498, то есть прямоугольный, – плоская фигура; ведь это треугольник, и он имеет прямой угол (рис. 4).
[5] Плоская фигура ν=σόπλευρος 499 – правильная (recta) и построенная ниже (рис. 5).
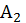
[ Телесных фигур пять.]
[1] (3) Сфера (sphaera) есть фигура, образованная в округлом, равная во всех частях (рис. 6).
[2] Куб (cubus) есть собственно телесная фигура, которая содержится в длине, ширине и высоте (рис. 7)500.
[3] (4) Цилиндр (cylindrus) есть квадратная фигура, имеющая сверху полукруг (рис. 8)501.
[4] (5) Конус (сопоп) есть фигура, которая сужается от широкого [основания], как прямоугольный [треугольник] (рис. 9)502.
[5] (6) Пирамида (pyramis) есть фигура, которая остро сходится от широкого [основания], ведь у греков огонь называется πυ̂ρ (рис. 10)503.
(7) И как любое число есть в504 10,505 так внутри этого круга содержатся контуры всех фигур506 (см. рис. на с. 128). Первая же фигура в их, [геометров,] искусстве – точка (punctus), которая не имеет частей. Вторая – линия (linea) – длина без ширины. Прямая линия – это такая, которая лежит равномерно (ex aequo) в своих точках. А поверхность (superficies) – это то, что имеет только длину и ширину. Границы поверхностей – это линии, контуры (formae) которых потому не были установлены [=названы] среди десяти вышеназванных фигур, что они находятся среди них507.
Глава XIII. О [средних] геометрических числах
При помощи же геометрии так ищешь [средние] числа508: ведь перемноженные крайние дают ту же [величину], что и перемноженные средние. Например, перемноженные VI и XII дают семидесяти двойное число, и столько же дают перемноженные [искомые] средние [числа] VIII и IX.
Глава XIV. Представление фигур, нарисованных ниже
509
Также при помощи восьми фигур получается другой смысл (ratio) в движении светил (stellae): или что они [знаки Зодиака] оппозиционные, или квадратурные, или тригональные, или секстильные, или соседние, или вместе, или окружающий (circumferens), то есть который или переходит или не достигает. Оппозиционные (diametra) – когда разделяются пятью знаками; квадратурные (quadrata, tetragona) – когда двумя; секстильные (hехаgona) – одним; соседние (asydenta) – когда ни одним; вместе (simul) – когда находятся в той же части; переходящий (superferens) – когда превосходит или совершает действие (actum facit); не достигает (superfertur) – когда предшествует; тригональные (trigona) – когда [разделяются] тремя средними.
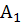
(2) Также в другом смысле есть восемь различий: знак [Зодиака], части, границы, [планеты] в соединении (conventu), прямое или попятное движение [планет], [их] широта (latitudo) и долгота (longitudo).
(3) Смысл внутренней формы. В этом отношении может возникнуть такой вопрос. [Почему] хотя в порядке числа первое – VIII, прежде него помещается IX, ибо в арифметическом или геометрическом смысле VIII больше IX. Ведь VIII – это куб, или объем, то есть тело, и больше этого открыть невозможно510. IX же есть поверхность [=квадрат], то есть вещь, которая не полна и не достигает совершенства. (4) Здесь, таким образом, находятся два куба, то есть два тела511.
Шестерка есть первое совершенное число512, ведь оно делится соответствующими (pares) числами так: на шестую [часть] – единицами (per as); на треть – двоицами (per dupondios): три раза по два – шесть, напополам [тройками], то есть два раза по три – шесть. Найди другое [число], которое так можешь разделить соответствующими числами, – это будет соответствовать намерению.
(5) Между первым [числом] по порядку […]513, то есть IX, которое посредством первого совершенного числа, в первую очередь умножая шесть раз по девять
То, что материя имеет такое количество частей, познается по справедливости двумя [пропорциями?], из которых она имеет одну в таком порядке: I, II, III, IV, IX, VIII и вместе с ними XXVII514.
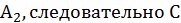
Титул III. О музыке
Глава XV. О музыке и ее имени
Музыка (musica) есть опытность в ритмах (modulationes), состоящая из звука (sonus) и пения (cantus). И названа музыкою как производное от Муз. Музы же названы α=πὸ του᾿ μάσαι, то есть «от искания (quaerendum)»515, поскольку через них, как полагали древние, отыскивается смысл ритма песен (carmines) и голосов. (2) При этом звук, поскольку он является вещью чувственно воспринимаемою, протекает с течением времени и запечатлевается в памяти. Потому у поэтов так придумано, что Музы – дочери Юпитера и Памяти. Ведь если звуки не удерживаются человеческою памятью, то они погибают, поскольку не могут быть записаны516.
Глава XVI. Об изобретателях ее
Моисей говорит, что открывателем искусства музыки был Иувал517. В рукописи в двух местах стоит именно Тувал (тж. в гл. 22), но трудно себе представить, чтобы христианский епископ не знал Библии и путал родоначальника музыкантов с родоначальником кузнецов (Быт. 4:21–22).), который был потомком Каина до потопа. Греки же говорят, что изобрел начала этого искусства Пифагор от звона молотков и ударов по натянутым струнам518. Другие передают, что Лин из Фив и Зет с Амфионом519 первыми прославились в музыкальном искусстве. (2) После них эта наука постепенно была чрезвычайно выстроена и расширена на многие лады, и было настолько же постыдно не знать музыки, насколько и букв. Употреблялась же она не только в священных делах, но и во всех праздничных, во всех веселых или более печальных делах. (3) Ведь как при почитании богов поются гимны, так на свадьбах – гименеи, на похоронах – френы и плачи под [звуки] флейт. На пирах же были распространены лиры или кифары, и для всех возлежащих устраивался пиршественный род песенок.
Глава XVII. Что может музыка
Итак, никакая наука не может быть совершенною без музыки, ведь ничего [не бывает] без нее. Ибо и сам мир, говорят, составлен из некой гармонии звуков, и само небо вращается в гармоничном ритме (modulatio). Музыка движет страстями, вызывает различное состояние чувства. (2) Также и в битвах пение трубы приободряет сражающихся, и насколько мощнее будет этот звук, настолько сильнее в схватке станет дух. Ведь именно пение ободряет гребцов, и в переносимых трудах музыка облегчает душу, и в каждом деле ритм (modulatio) голоса снимает усталость. (3) Также и возбужденные души успокаивает, как говорят про Давида, который избавил Саула от нечистого духа искусством ритма (modulatio). Также и животных, равно ползающих, летающих и дельфинов, музыка своими ритмами побуждает к слушанию. И что бы мы ни говорили и как бы мы ни возбуждались из-за пульсов внутри вен, считается, что [это] связано с силами гармонии через музыкальные ритмы (rhythmi).
Глава XVIII. О трех частях музыки
У музыки три части, то есть гармоника, ритмика и метрика. Гармоника (harmonica) – это та, которая разрешает звуки в высокий (acutus) и низкий (gravis). Ритмика (rhythmica) есть та, которая исследует столкновение слов: хороший ли [получается] звук или они плохо связываются. (2) Метрика (metrica) есть та, которая правдоподобным образом познает меры (mensurae) различных [стихотворных и музыкальных] метров, как, например, героического, ямбического, элегического и прочих520.
Глава XIX. О тройном разделении музыки
О каждом же звуке, который есть материя песен, известно, что он имеет троеобразную природу. Первая есть гармоника, которая состоит из звука у песен. Вторая – органика (organica), которая состоит из дутья (flatus). Третья – ритмика, которая включает ритмы (numeri) от удара пальцев521. (2) Ведь звук издается или голосом, то есть при помощи горла, или дутьем, то есть при помощи труб или флейт, или ударом, то есть при помощи кифары или всякого иного [инструмента], в который ударяют певцы522.
Глава XX. О первом разделе музыки, который называется гармоникою
Первый раздел музыки, который называется гармоникою, то есть ритмом (modulatio) голоса, касается комиков, трагиков или хоров, или всех, кто поет собственным голосом. Он получает движение от души и тела, и от движения звука, из которого складывается музыка, которая применительно к человеку называется голосом. (2) Голос (vox) есть воздух, толкаемый (колеблемый, verberatus) дыханием, от чего и наречены глаголы (verba)523. Свойствен же голос человеку и неразумным животным. Ибо у иных [звучащих вещей] не в собственном смысле звучание называется голосом, как, [например] «взревел голос трубы» [или]
...Глас, от брега отраженный (Verg., Aen., III, 556).
Ибо в собственном смысле должно быть, чтобы на берегу скалы «звучали», и
Тут в отдаленье труба пропела звучанием грозным
(Verg., Aen., IX, 503).
Гармония (harmonia) есть ритм (modulatio) голоса и согласовывание многих звуков, или взаимное их приспособление.
(3) Созвучие (symphonia)524 есть соразмерность ритма из высоких и низких согласующихся звуков, [возникающих] и в голосе, и при дутье, и при ударе. Очевидно, что с ее помощью голоса более высокие согласуются с более низкими так, что если какой из них не будет находиться в согласии с нею, то он будет бить по чувству слуха.
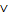
Ее противоположность есть диафони́я (diaphonia), то есть голоса, [звучащие] нестройно, разногласно.
(4) Благозвучие (euphonia) есть сладость голоса, потому оно и названо «мелос»525 от сладости и мёда (mel).
(5) Диа́стема (diastema) есть интервал голоса, связанный с [=лежащий между] двумя или более звуками.
(6) Диезы (diesis) суть некие интервалы и переводы (deductiones) ритмизирования, а также переходы из одного звука в другой526.
(7) Тон (tonus) есть резкое издание голоса. Ведь у гармонии есть различие и количество, которое для голоса состоит в звучании (accentus) или напряжении (tenor) [=высоте]. Его рода музыканты разделили на пятнадцать частей, из которых гиперлидийский – новейший и самый высокий, а гиподорийский – самый низкий527.
(8) Пение (cantus) есть изгибание голоса, ведь звук является прямым, а звук предшествует пению.
(9) Арсис (arsis) есть повышение голоса, и это есть начало [такта].
Тесис (thesis)528 есть понижение голоса, и это – окончание [такта]529.
(10) Сладкие (suaves) голоса суть тонкие и густые, отчетливые и резкие (acuti).
Ясные (perspicui) голоса суть те, которые протягиваются дольше так, что непрерывно заполняют все пространство, как, например, звук труб.
(11) Тонкие (subtiles) голоса суть те, в которых нет дыхания, как это бывает у детей или у женщин, или у больных, как, например, [звуки] струн (nervi). Они ведь самые тонкие у кишечных струн (chordae), [которые] издают тонкие и мягкие звуки.
(12) Жирные (pingues) голоса – это когда одновременно [с голосом] издается много дыхания, как, например, у мужчин.
Резкий (acutus) голос есть более тонкий, высокий, какой, например, мы видим у кишечных струн.
Жесткий (durus) голос есть тот, который издает звуки сильно, как, например, гром или как звук наковальни, поскольку молоток бьет о жесткое железо.
(13) Грубый (asperus) голос есть хриплый и тот, который рассыпается на маленькие и не лишенные сходства толчки.
Слепой (caecus) [ глухой] голос есть тот, который, будучи издан, скоро умолкает, а также тот, который производится дольше [но] несколько удушенным, как, например, [звук] в глиняных сосудах.
Заливистый (vinnolus) голос есть мягкий и извивающийся; и назван так от завитка (vinnus), то есть мягко вьющихся кудрей.
(14) Совершенный же голос – высокий, сладкий и отчетливый: высокий, чтобы до высоты доставал, отчетливый, чтобы уши наполнял, сладкий, чтобы души слушающих ласкал. Если чего-то из этого недостает, то голос не является совершенным.
Глава XXI. О втором разделе музыки, который называется органикою
Второй раздел, органика, касается тех [инструментов], которые, будучи полностью наполнены дыханием, оживляются в звук голоса, как трубы, свирели, дудки, орга́ны, пандуры и им подобные инструменты.
(2) Слово «орга́н» (organum) есть общее для всех музыкальных орудий. Тот же, к которому прилагается мех, греки называют другим именем. То же, что он называется органом, – это, по мнению греков, сильная вульгарность530.
(3) Труба (tuba) впервые изобретена этрусками, о чем [пишет] Вергилий:
Ревом тирренской трубы огласилися неба просторы (Verg., Aen., VIII, 526).
Употребляются же они не только в битвах, но и во все праздничные дни из-за блеска прославления и веселья531. Почему и в Псалтири говорится: «Трубите в новомесячие трубою, в определенное время, вдень праздника нашего» (Пс., 80:4). Предписано ведь было иудеям, чтобы в начале новой луны звучали трубы, что делают даже до сих пор.
(4) Открытие флейт (tibiae) произошло во Фригии. Их когда-то давно использовали только на похоронах, а сегодня и в священнодействиях язычников. Полагают, что они названы флейтами, потому что первоначально делались из оленьих берцовых костей (tibiae) и голеней оленят, после же они в несобственном смысле стали так называться, поскольку уже не делались из голенных костей. Отсюда и [слово] «флейтист» – как бы играющий на флейтах532.
(5) Имя «свирель» (calamus, тростник) – это собственное имя растения, и названа она так от волнения, то есть растекания голоса.
(6) Дудка (fistula), как одни полагают, была некогда изобретена Меркурием, а другие – Фавном, которого греки называют Паном; некоторые же считают, что Идасом, пастухом из Агригента в Сицилии. Названа же она дудкою, так как испускает голос. Ведь у греков голос называется φω̂ς, а «испущенный» – στολία533.
(7) Самбук (sambuca) в представлении музыкантов свойствен оркестрам (symphoniae). Ведь самбук (бузина) – род хрупкого дерева, из которого делаются и флейты.
(8) Пандура (pandorium) названа от изобретателя, о чем Вергилий:
Первым Пан изобрел скрепленные воском тростинки (calami),
Пан, предводитель овец и нас, пастухов, повелитель
(Verg., Eel., И, 32–33).
Был ведь у язычников пастушеский бог, который первым разные [по длине] тростинки приспособил для пения, и сложил с усердным искусством534.
Глава XXII. О третьем разделе музыки, который называется ритмикою
Третий раздел есть ритмика, касающаяся струн и ударов, которому приданы различные виды кифар, а также тимпан, кимвал, систр, чашечки медные и серебряные, или другие, которые, если в них ударить металлической твердостью, отзываются сладким звоном, и прочие этого рода [инструменты].
(2) Открывателем кифары и псалтерия был, как говорят, Иувал535. В нашем синодальном переводе Библии кифара названа гуслями(Быт., 4:21).), что сказано выше. Затем же, по мнению греков, считается, что использование кифары было открыто Аполлоном536. Рассказывают, что первоначально форма кифары была похожа на человеческую грудь, и названа так по той причине, что как голос издается из груди, так и из нее – пение. Ведь грудь на дорийском наречии называется κιθάρα. (3) Постепенно же появились многие ее виды, как, например, псалтерии, лиры, барбиты, финикийские, пектины537 и те, которые именуются индийскими, на которых двое бряцают одновременно. И еще, и еще, и квадратной формы и треугольной. (4) Число струн умножалось, и [их] род изменялся. Древнейшие [люди] называли кифару fidicula, или fides, ибо настолько точно между собой соединены ее струны, насколько существуют хорошие отношения у тех [людей], у которых есть доверие (fides). Древняя же кифара была семиструнною, почему и Вергилий [говорит]:
…[Вторит пению] разделенным на семь [частей] голосом (Verg., Aen., VI, 656).
(5) «Разделенным» же потому, что никакая струна с соседнею струною не издает одинаковый звук. А струн семь, или поскольку они весь голос [ октаву] исчерпывают, или поскольку небо движется семью движениями538. (6) Кишечные струны (chordae) же названы от сердца (сог), ибо как сердцу в груди присуще пульсирование, так и струне в кифаре. Их первым выдумал Меркурий, потому что раньше звук исходил от жил (nervi).
(7) Псалтерий (psalterium), который в простонародье называется песенником (canticum), получил имя от щипания [струн], и его голосу хор созвучно отвечает. [У него] есть сходство с варварскою кифарою в виде буквы Δ, но между псалтериями и кифарами есть то различие, что псалтерий имеет вверху то выдолбленное дерево [резонатор], откуда исходит звук, и в струны [на ней] бьют внизу, и они звучат верхними [концами]. А кифара выдолбленное дерево имеет снизу. Евреи же используют десятиструнный псалтерий – по числу заповедей Декалога.
(8) Лира (lyra)539 называется α=πὸ τοὺ λυρει̂ν, то есть «от разнообразия голосов», которое достигается разными звуками. Говорят, что лира впервые была изобретена Меркурием таким образом. Когда Нил вернулся в свое русло, на полях остались разнообразные животные, осталась и черепаха. Поскольку она сгнила, а жилы ее сохранились натянутыми внутри панциря, то, когда в нее ударил Меркурий, она издала звук. По этому образцу Меркурий изготовил лиру и передал ее Орфею, который после этого стал наиболее искусным в отношении этой вещи. (9) Почему и считается, что при помощи этого искусства пение своими ритмами подчиняет не только диких зверей, но и скалы, и леса. Музыканты из любви к занятию и ради восхваления песни даже придумали, измышляя свои басни, что лира находится среди созвездий.
(10) Тимпан (tympanum)540 есть шкура или кожа, натянутая на дерево с одной стороны. Он ведь есть половина симфонии, наподобие решета. Тимпаном же назван, поскольку он средний, откуда и средний [по качеству] жемчуг называется тимпаном, и в него самого, как и в симфонию, бьют палочкой.
(11) Кимвалы (cymbala)541 суть некие чашечки, которые, если в них ударить, бьются друг о друга и издают звук. Названы же кимвалами, ибо они одновременно колеблются как в танце, ведь греки танцы называют κύμβαλα.
(12) Систр (sistrum)542 назван по имени изобретательницы. Ведь считается, что Исида, царица египетская, изобрела этот род [инструментов]. Ювенал, [например, пишет:]
Пусть хоть Исида разит мои очи разгневанным систром
(Iuven., Sat., XIII, 93).
Потому в него и бьют женщины, что изобретательница этого рода [инструментов] – женщина. Отчего и амазонки систром призывали женщин на войну.
(13) Колокольчик (tintinabulum) имеет имя от звука [своего] голоса, как, например, <и> хлопок (plausus) рук, и скрип (stridor) двери.
(14) Симфония (symphonia) называется в простонародье полым деревом, и она с обеих сторон затянута кожею. Когда музыканты бьют палочками сюда и туда, в ней получается сладчайшее пение из согласия низкого и высокого [звучания].
Глава XXIII. О [средних] музыкальных числах
При помощи же музыки так ищешь [средние] числа: возьмешь крайние, например VI и двенадцатерицу, посмотришь, на сколько единиц XII превосходит VI, то есть на VI единиц, возводишь [это последнее число] в квадрат: шесть раз по шесть дают XXXVI. Сложишь те первые крайние, VI и XII, вместе получится XVIII. Разделишь тридцать шесть на восемнадцать, получится двоица. Его прибавишь к меньшему крайнему, то есть к шестерке, получится VIII, и это будет среднее [гармоническое] между VI и XII.543 Вот почему VIII превосходит VI на две единицы, то есть третью часть от VI, и XII превосходит VIII на IV единицы, то есть [свою] третью часть. На какую, следовательно, часть оно превосходит, на такую и его превосходят.
(2) И подобно тому, как в мире это отношение (ratio) является из обращения [небесных] сфер, так и в микрокосме во всем, не только в голосе, оно пребывает, так что не существует человека без этого совершенства, обходящегося без музыки. В том же музыкальном совершенстве состоят еще и стихи, в арсисе и тесисе, то есть в повышении и понижении [голоса].
Титул IV. Об астрономии
544
Глава XXIV. Об имени астрономии
Астрономия (astronomia) есть закон звезд (astrae), который исследовательским способом касается движений созвездий (sidera) и [их] фигур и обращения светил (stellae)545 вокруг себя и вокруг Земли.
Глава XXV. Об изобретателях ее
Первыми астрономию изобрели египтяне. Об астрологии же и о наблюдении за временем рождения первыми стали учить халдеи. Автор Иосиф утверждает, что Авраам наставил египтян в астрологии546. Греки же говорят, что это искусство было впервые выдумано Атлантом потому, что он, говорят, поддерживал небо. Но кто бы он ни был, побуждаемый движением неба и рассудком души, он при помощи смены времен, при помощи неизменных и определенных движений светил, при помощи размеренных величин интервалов рассмотрел некие размеры и числа, которые он нашел, связывая [их] с астрологией, определяя и отделяя по порядку.
Глава XXVI. О наставниках ее
Хотя на обоих языках об астрономии разными [людьми] написаны свитки, среди них, однако, у греков выдающимся считается Птолемей, царь александрийский547: ведь он установил правила, по которым находят движение светил.
Глава XXVII. О различии астрономии и астрологии
Между астрономией и астрологией есть некоторое различие. Ведь астрономия охватывает обращение неба, восходы, заходы и движения созвездий, или по какой причине они так называются. Астрология (astroligia) же – [наука] частично природная, частично суеверная548. Природная – когда следует движениям Солнца и Луны или определенным по времени положениям светил. Суеверная же есть та, которой следуют звездочеты (mathematici), которые гадают по светилам и которые также распределяют двенадцать небесных знаков [Зодиака] по отдельным частям тела и души549, и пытаются по движению созвездий предсказывать гороскопы (nativitates) и нравы людей.
Глава XXVIII. О смысле астрономии
Смысл (ratio) астрономии заключен в многом. Ведь она определяет, что́ есть мир, каково положение и движение [небесных] сфер, что́ есть небесные ось и полюса, каковы области неба, что есть движение Солнца, Луны и звезд, и прочее.
Глава XXIX. О мире и его имени
Мир (mundus) есть то, что состоит из неба, земли и моря, окруженных созвездиями. И он потому назван миром, что всегда находится в движении (motus); ведь никаким его частям не дано находиться в покое.
Глава XXX. О форме мира
Форма [земного] мира описывается так. Ведь каким образом мир поднимается к северной области, таким склоняется к южной. Голова его и как бы лицо – это восточная область, а задняя часть – северная550.
Глава XXXI. О небе и его имени
Философы говорят, что небо (caelum) круглое, вращающееся и пламенное. И называется оно этим именем потому, что оно имеет оттиснутые значки светил как на чеканной (caelatum) вазе. (2) Ведь Бог усыпал его яркими светильниками, и поставил светящиеся Солнце и, конечно, диск Луны, и украсил его сверкающими значками искрящихся звезд. А по-гречески оно называется ου=ρανός [от] α=πὸ του̂ ὁράσθαι, то есть «от ви́дения»551, потому что воздух прозрачен и более чист для созерцания.
Глава XXXII. О положении небесной сферы
Сфера неба (sphaera caeli) [=сфера звезд]552 есть некий образ, оформленный как круг, равный во всех частях, центр которого – Земля. Говорят, что у этой сферы нет ни начала, ни конца, потому что она [заключена] в округлом – как бы окружность, для которой непросто понять, где она начинается и где заканчивается. (2) Философы же ввели семь небес мира, то есть планет, при помощи согласного движения [их] шаров, все из которых, как рассказывают, связаны [своими] кругами (orbes), и про эти [круги] полагают, что они, опираясь на себя и будучи словно вложенными, поворачиваются назад, и [вместе с тем], наоборот, подхватываются движением других [кругов]553.
Глава XXXIII. О движении той же сферы
Вращательное движение (motus) сферы совершается посредством двух полюсов (axes), из которых один – Северный, который никогда не заходит и называется Борейским, другой – Южный, который никогда не виден554 и называется Австронотийским.
(2) Говорят, что при помощи этих двух полюсов (poli) движется небесная сфера, и вместе с ее движением созвездия, закрепленные на ней, кружатся от востока к западу, совершая на севере более короткие круги вокруг центра.
Глава XXXIV. О беге той же сферы
Сфера неба поворачивается от восхода к закату единожды в день и ночь за двадцатичетырехчасовые промежутки [времени], за которые Солнце, вращаясь, завершает свой бег над землею и под землею555.
Глава XXXV. О быстроте [вращения] неба
Говорят, что сфера неба движется с такой быстротой, что, если только светила перестанут мчаться навстречу стремительному ее бегу так, чтобы задерживать ее, она обратит мир в развалины.
Глава XXXVI. Об оси неба
Ось (axis) [мира] есть северная прямая линия, которая проходит через середину шара (pila) сферы; и названа она осью потому, что вокруг нее сфера поворачивается как колесо, или поскольку там есть [созвездие] Возок556.
Глава XXXVII. О небесных полюсах
Полюса (poli) [мира] суть маленькие окружности, которые вращаются по оси [мира]. Из них один – Северный, который никогда не заходит, и называется Борейским, другой – Южный, который никогда не виден, и называется Австронотийским. И названы они полюсами, поскольку они ступицы (cycli) оси, как это делается в повозках, то есть именуются от шлифования (poliendum)557. Но Борейский полюс виден всегда, Австронотийский же никогда, ибо все правое на небе расположено выше, а южное опущено.
Глава XXXVIII. О точках вращения неба
Точки вращения (cardines) неба – это крайние части оси [мира]. И названы они так потому, что с их помощью поворачивается небо, или поскольку они вертятся как сердце (cor).
Глава XXXIX. О небесном своде
Свод (convexa) же неба есть его край, названный [так] от изгиба (curvitas), как, [например], следующее:
Сколько уж раз своды неба окутались влажною ночью.
Ведь сводчатое – это изогнутое (curvum), как бы повернутое (con-versum) и наклоненное, и искривленное в виде круга.
Глава XL. О вратах неба
Врат (ianuae) неба два – восточные и западные. Ведь через одни врата Солнце выходит, а через другие уходит назад.
Глава XLI. О двойном лице неба
Лицо (facies) неба, или голова, – это восточная область, а крайняя [часть] – северная. О чем Лукан:
Так же лежит и конечная часть Вселенной под гнетом Вечной зимы и снегов (Lucan., Phars., IV, 106–107).
Глава XLII. О четырех частях неба
Областей (climata) неба, то есть сторон или частей, четыре, из коих первая часть восточная, поскольку там восходят некоторые светила; вторая – западная, где у нас заходят некоторые светила; третья – северная, куда Солнце приходит с более длинными днями; четвертая – южная (australis), куда Солнце приходит, когда ночи длиннее [дней]558. (2) Восток (Oriens) наречен от появления (ex-ortum) Солнца. Запад (Occidens) – поскольку он делает так, что день как бы погибает (occiditur) и гаснет. Ведь он скрывает свет мира и напускает мрак. Север (Septentrio) же назван от семи (septem) звезд полюса (axis), которые, поворачиваясь, кружатся в нем самом559. Он справедливо называется также центром вращения (vertex) [мира] потому, что вращается (vertitur). (3) Полдень (Meridies) же назван [так] или поскольку в этом месте Солнце делает середину дня, как бы «полудень», или поскольку в это время эфир сверкает (micat) чище.
(4) Есть и другие семь параллелей (climata) неба, как бы семь линий от востока до запада, под которыми особым [для каждой] образом производятся различные нравы людей и разные животные и которые названы от наиболее известных своих мест. Из коих первая – Мероэ (Merois), вторая – Сиена, третья – Нижний Египет (Catachoras), то есть Африка, четвертая – Родос, пятая – Геллеспонт, шестая – Месопонт, седьмая – Борисфен (Borusthenes)560.
Глава XLIII. О полусферах
Полусферы (haemisphaeria) – это половинные части сферы. Надземная полусфера есть та часть неба, которая нам полностью видна; подземная полусфера есть та, которую невозможно видеть, [так] как днем она бывает под землей.
Глава XLIV. О пяти кругах неба
Поясов (zonae) неба пять561. Некоторые из них, более умеренные части, отличаются тем, что населены, а некоторые из-за свирепого холода или жары остаются незаселенными. Каковые потому называются поясами или кругами, что существуют в круговращении [небесной] сферы.
(2) Из них первый круг потому называется α=ρκτικόί (арктическим), что в нем просматриваются включенные [в него] знаки Арктов562.
Второй круг – θερινός (жаркий), который зовется τροπικός; (тропическим, поворотным), поскольку Солнце, принося лето в аквилонские [=северные] пределы, за этот круг не выходит, но тотчас поворачивается, и поэтому он называется τροπικός.
(3) Третий круг – ι=σημερινός (экваториальный), который латинянами потому называется равноденственным (aequinoctialis), что Солнце, пребывая в этом круге, совершает равноденствие. Ведь ι=σημερινός («равнодлительным») по-латыни называются и день и ночь [во время равноденствия]. В этом круге, будучи установленной, ясно просматривается половинная часть сферы [неба].
Четвертый же круг назван α=νταρκτικόσ (антарктическим) потому, что является противоположным тому кругу, который мы называем α=ρκτικόσ.
(4) Пятый круг – χειμερινός τροπικός; (зимний тропический), который латинянами называется зимним или [кругом] зимнего солнцеворота (brumalis), потому, что Солнце, пребывая в этом круге, приносит зиму тем, которые живут у Аквилона, и лето – тем, которые живут в южных частях [света].
Глава XLV. О круге Зодиака
Зодиак (Zodiacus) же есть круг, который состоит из углов пяти линий <и> из одной линии563.
Глава XLVI. О белом круге
Круглый Млечный Путь (Lacteus Via), который виден на [небесной] сфере, назван так от белизны, поскольку он белый. Как говорят некоторые, это есть путь, по которому кружится Солнце, и светит он так, перенимая его сияние564.
Глава XLVII. О величине Солнца
Величина Солнца (Sol) больше (fortior) [величины] Земли, поэтому в то мгновение, когда восходит, оно одновременно показывается равно на востоке и на западе565. А то, что оно кажется нам [диаметром] примерно с локоть, надлежит понимать, поскольку Солнце [далеко] отстоит от Земли; и из-за этого расстояния получается так, что оно кажется нам маленьким.
Глава XLVIII. О величине Луны
Сообщают также, что величина Луны (Luna) меньше [величины] Солнца. Ведь пока Солнце выше Луны566, оно все-таки кажется нам [несколько] больше Луны, однако если его приблизить к нам, оно покажется много больше Луны. И подобно тому, как Солнце мощнее Земли, так и Земля мощнее Луны на некоторую величину567.
Глава XLIX. О природе Солнца
Пока Солнце является огненным, оно из-за чрезмерного движения при обращении еще больше раскаляется. Философы говорят, что его огонь питается водою568 и получает от [этого] противоположного элемента энергию (virtus) света и теплоты. Поэтому мы чаще видим его влажным и источающим росу.
Глава L. О движении Солнца
Солнце движется569 само собою, а не вращается вместе с миром [=сферою звезд]. Ибо если бы оно оставалось на небе неподвижным, все дни и ночи были бы равными, но поскольку мы видим, что оно завтра зайдет в одном месте, а вчера восходило в другом, очевидно, что оно движется само собою, а не вращается вместе с миром. Ведь оно совершает годичные круги за неравные промежутки вследствие смен времен (mutationes temporum) [года]. Восходя, оно делает день, заходя, приводит ночь. (2) Ибо, уходя далеко на юг, оно делает зиму (hiems), чтобы [наша] земля напиталась от зимней влаги и снега. Приближаясь само к полюсу, оно возвращает [нам] лето (aestas), чтобы урожай созрел спелым и те [овощи и плоды], которые варятся во влаге570, размягчались от нагревания.
Глава LI. О действии Солнца
Солнце, восходя, делает день, заходя, приводит ночь, ведь день (dies) – это Солнце над землею, ночь (nox) – Солнце под землею. От него ведь [происходят] часы. От него – день, когда оно восходит, от него же и ночь, когда заходит. От него считают месяцы и годы. От него происходят смены времен [года]. (2) Когда же оно движется на юг, оно ближе к земле, когда же оно вблизи севера, оно поднимается выше571. <Ему, поэтому, Бог установил различные пути (cursus), места и времена, чтобы, оставаясь всегда на одном и том же месте, оно своим ежедневным жаром не уничтожило [землю], и как говорит Климент572: «[Солнце] получает различные пути, посредством которых в зависимости от последовательности времен [года] регулируется правильное устройство климата (аег) и сохраняются в порядке чередование и перемена [времен]. Ибо пока оно восходит к высотам, стоит весна. Там, где доходит до вершины, оно пылает летним жаром. Спускаясь назад, возвращает осеннюю умеренность. Там же, где возвращается в нижнюю [часть] круга, оно из ледяных скреп неба оставляет нам холод зимней стужи».>
(Далее следует круглый чертеж, который в середине имеет центр мира [Ο], а вокруг него – положения Солнца, подписанные так: «Это восход Солнца в Рождество Господне» [Δ]; «Шестой час дня» [Θ]; «Заход в Рождество Господне» [Γ]; «Заход в равноденствие» [Α]; «Заход Солнца в Рождество Иоанна» [Ε]; «Постоянная полночь» [Η]; «Восход Солнца в Рождество Иоанна» [Ζ]; «Это восход Солнца в равноденствие» [Β].)573
Глава LII. О пути Солнца
Солнце, восходя, держит путь на Полдень. Затем оно достигает Запада и омывается Океаном, ходит по неизвестным дорогам под землею, и снова возвращается к Востоку.
Глава LIII. О свете Луны
Некоторые философы говорят, что Луна имеет собственный свет574: одна часть ее шара является сияющею, а другая – темною, <так:
>, и, постепенно поворачиваясь, она образует различные фазы (formae). (2) Другие, напротив, утверждают, что Луна не имеет своего света, но освещается лучами Солнца. Поэтому она и претерпевает затмение, если между нею и Солнцем проходит тень Земли. <Ведь Солнце находится выше этого места. Отсюда получается, что, когда [Луна] находится под ним, то светится в верхней части; в нижней же, которая обращена к земле, она затемнена.>
Глава LIV. О фазах Луны
Первый вид Луны – двурогий, так:
.Второй – с [серповидным] вырезом, <так>
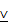
. Третий – половина, <так:>
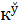
. Четвертый – полная <так:>
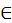
. Пятый – снова половина <сверху, так:>
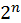
. Шестой – снова с вырезом, <так:>
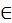
. Седьмой – двурогий, <так:>
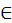
.
(2) Седьмой же с половиною [день лунного месяца] и двадцать второй с половиною – для ее диска средние
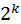
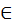
, а прочие[дни] – долевые575.
Глава LV. О новолунии
Время новолуния (interlunio) Луны есть время между угасанием и рождением Луны. Бывает же тридцатый день, когда Луна не светит. Ее потому в это время невозможно увидеть, что, находясь в соединении с Солнцем, она затемняется, но в то же мгновение, постепенно нарождаясь, она становится видимою, удаляясь от него.
Глава LVI. О движении Луны
Луна отмеряет месячные промежутки посредством смены убывающего и прибывающего света. Она потому движется по косой орбите (obliquus cursus), а не по прямой, как Солнце576, очевидно, чтобы не упасть в центр Земли; и она часто претерпевает затмение. (2) Ведь ее круг – соседний с кругом Земли. Возрастая, она располагается рогами на восток [т. е. налево], убывая, – на запад [т. е. направо]. И правильно: ибо свет [ее в последнем случае] будет заходить и убывать.
Глава LVII. О близости Луны к Земле
Луна ближе к Земле, нежели Солнце577. Потому она по более короткому кругу быстрее совершает свой путь. Ведь путь, который Солнце совершает за триста шестьдесят пять дней, она пробегает за тридцать дней. Потому древние располагали месяцы по Луне, а годы – по движению Солнца.
Глава LVIII. О затмении Солнца
Затмение (eclipsis) Солнца578 бывает, поскольку Луна на тридцатый [день месяца] попадает на ту же линию, по которой двигается Солнце, и, заградив ее собою, затемняет Солнце. Ибо нам кажется, что Солнце погасло, пока против него стоит диск Луны.
Глава LIX. О затмении Луны
Затмение Луны бывает, поскольку Луна входит в тень Земли. Ведь считается, что она имеет не свой свет, но освещается Солнцем, потому и претерпевает угасание, если между нею и Солнцем попадает тень Земли. (2) Претерпевает же его Луна на пятнадцатый [день месяца] до тех пор, пока не она не уйдет от центра и оттени противостоящей Земли и не увидит Солнца, или пока не будет увидена Солнцем.
Глава LX. О различии светил, созвездий и звезд
Светила, созвездия и звезды между собою различаются. Ибо светило (stella) есть что-либо единичное. Созвездия (sidera) же образованы многими (plurimae) светилами, как, [например,] Гиады, Плеяды. А звезды (astra) – это большие (grandes) светила, как, [например,] Орион, Волопас579. Но писатели эти названия смешивают и пишут «звезды» вместо «светила» и «светила» вместо «созвездия».
Глава LXI. О свете светил
Говорят, что светила не имеют собственного света580, но освещаются Солнцем, как и Луна.
Глава LXII. О положении светил
Светила [звезды] неподвижны и, будучи закреплены [на небесной сфере], переносятся вместе с небом вечным движением. И днем они не уничтожаются, но затмеваются блеском Солнца.
Глава LXIII. О движении светил
Светила (sidera) или переносятся, или движутся. Переносятся, когда закреплены на небе и вращаются вместе с небом. Некоторые же движутся, <как, например,> планеты, то есть «блуждающие» [светила], которые совершают свои отклоняющиеся, однако, точно определенные, пути.
Глава LXIV. О различном пути светил
Из светил, поскольку они перемещаются по различным небесным кругам, некоторые, быстрее взойдя, позднее заходят; некоторые, позднее взойдя, быстрее склоняются к закату; иные одновременно восходят, но не одновременно заходят; однако все в свое время возвращаются на собственный путь.
Глава LXV. О расстояниях до светил
Светила сами по себе отстоят от Земли на различные расстояния, потому они кажутся для наших глаз [имеющими] неодинаковый блеск (claritas): больший или меньший. Ибо много меньшие581 [расстояния] – у тех [светил], которых мы видим заметными, но те, что расположены дальше, нам видны хуже.
Глава LXVI. О круговом числе светил
Круговое число (numeruscircularis) светил – это такое [число], по которому, как говорят, познается то, за какое время каждое светило обежит свой круг или по долготе, или по широте582. (2) Ибо Луна, как сообщают, выполняет свой круг за целый год, Меркурий – за XX лет, Светоносец [Венера] – за IX лет, Солнце – за XIX лет, Вечерняя звезда [Марс] – за XV <лет>, Фаэтон [Юпитер] – за XII лет, Сатурн – за XXX <лет>583. Закончив их, они возвращаются к началу (reversio) своего круга в тех же знаках [Зодиака] и частях [земного года].
(3) Некоторые светила (sidera) [планеты] из-за лучей Солнца совершают аномалии задержки [движения], или попятного [движения], или стояния, в связи с чем поэт упоминает [следующее], говоря:
…Время года вам Солнце меняет,
Ночью сменяет вам день, планетам лучей своих мощью
Путь заграждает вперед и стоянкой их ход замедляет584
(Lucan., Phars., 201–203).
Глава LXVII. О светилах-планетах
Некоторые светила потому называются планетами (planetae), то есть «блуждающими»585, что они по всему миру различным движением бегают туда и сюда. Отчего – из-за того, что блуждают, – говорят, что они движутся вспять, или совершают аномалии, то есть когда принимают или теряют частицы [солнечного света, огня]. Далее, когда только теряют, говорят, что они движутся вспять (retrograda); и они совершают стояние, когда стоят.
Глава LXVIII. О предшествовании и прямом движении светил
Предшествование (praecedentia), или прямое движение (antegrada-tio) светил [планет], бывает, когда кажется, что светило находится в собственном движении, и что-то против обыкновения [ему] предшествует586.
Глава LXIX. Об удалении и попятном движении светил
Удаление (remotio), или попятное движение (retrogradatio) светил [планет], – это такое, при котором светило, находясь в собственном движении, одновременно кажется двигающимся вспять.
Глава LXX. О стоянии светил
Стояние (statio, status) светил [планет] бывает тогда, когда светило, хотя и движется не переставая, кажется стоящим в некоторых местах.
Глава LXXI. Об именах светил, которые получили имена небеспричинно
Солнце (Sol) названо [так] потому, что оно одно (solus) видимо [на небе], когда все звезды (sidera) затемнены его сиянием.
(2) Луна (Luna) – это как бы Луцина без среднего слога. О чем Вергилий, [обращаясь к Диане]:
Чистая дева Луцина! (Verg., Eel., IV, 10).
Получила же она имя как производное от света (lux) Солнца потому, что получает от него освещение и отдает полученное.
(3) Звезды (stellae) наречены от стояния (standum), поскольку они всегда стоят закрепленными на небе и не падают. Ибо когда мы видим, что звезды как бы падают, – это не звезды, но выпавшие из эфира огоньки, которые бывают, когда ветер, устремляющийся все выше, увлекает за собою [при последующем падении] эфирный огонь, который в этом своем состоянии похож на падающие звезды587. Ибо звезды падать не могут, ведь они, как сказано раньше, неподвижны и, будучи закреплены, переносятся небом.
(4) Созвездия (sidera) наречены потому, что мореплаватели, разглядывая (considerare) их, направляют [свои суда] по выбранному курсу, чтобы не оказаться в каком-либо ином месте из-за обманчивых волн и ветров. Некоторые же светила потому называются «знаками» [=созвездиями], что их наблюдают моряки у рулевых весел, изучая их расположение и блеск, и через эти вещи открывается будущее положение неба. (5) Но и все люди наблюдают их, чтобы предвидеть качества воздуха [=погоду] летом и зимою, весною и осенью. Ведь они обозначают качество времен через определенные места своего восхода и заката.
(6) Первый из знаков – это Аркт (Arcton)588, который, будучи закреплен на оси [мира], вращается как семь обращающихся звезд. Это имя – греческое, по-латыни оно значит «медведица»; наши ее называют Септентрионом (Septentrio), ибо она вращается на манер возка. (7) Ведь трионы в собственном смысле – это пахотные быки, и названы [так] потому, что топчут (terant) землю, – они как бы «топтуны» (teriones). То, что Септентрионы не заходят, получается из-за соседства с осью [мира], ибо они находятся на ней.
(8) Медвежий страж (Arctophylax)589 назван так потому, что следует за Арктом, то есть за Геликой-медведицей. Его же назвали Волопасом (Bootes) потому, что он постоянно сопровождает Возок. Этот знак состоит из многих ярких звезд, среди которых есть Арктур (Arcturus)590. (9) Звезда Арктур помещена за хвостом Большой Медведицы в знаке Волопаса. Названа же Арктуром, то есть как бы ̓ˊΑρκτου ου=ρά (хвост Медведицы), ибо она расположена в груди Волопаса. Восходит же в зимнее время.
(10) Орион (Orion) же сияет на юге за следами Тельца, и назван Орионом от наводнения (urina), то есть разлива воды591. Ведь, появляясь в зимнее время, он беспокоит море и земли дождями и бурями.
(11) Поэтому латиняне называют его Iugulum (поясом, перевязью), что значит «военный», как, [например] меч (gladius). Из звезд он имеет самый страшный и яркий свет. Если в нем сияют все [звезды], он предвещает ясную погоду, если же порядок его [звезд] затемнен, это означает, что грозит буря.
(12) Гиады (Hyades)592 названы α=πὸ του̂ ὑ᾿ ειν, то есть от влаги и дождя, ведь дождь по-гречески называется ὑετός. Ибо они своим восходом производят дожди. Почему и латиняне их именуют влажными, ибо, появляясь, они оказываются знаком дождей. О чем Вергилий:
Арктур и дождливые Гиады… (Verg., Aen., I, 744)
Это семь [звезд] перед Тельцом, и они восходят в весеннее время.
(13) Плеяды (Pliades)593 наречены от множества, ибо множество греки именуют α=πὸ του̂ πλείστου (от самого многочисленного). Это семь звезд за коленами Тельца, из которых видны шесть, а одна скрыта. Латиняне их называют Вергилиями (Vergiliae), обозначая время, то есть весну (ver), когда [эти звезды] появляются. Ибо заходом своим они обозначают зиму, а восходом – лето, время начала навигации.
(14) Звезда Собачка (Canicula), которая также именуется Сириусом (Sirius), в летние месяцы находится посредине неба, и пока Солнце восходит к ней, она связана с Солнцем, и его жар удваивается, а тела разрушаются и [из них] выпаривается влага. Поэтому от этой звезды названы дни каникул, когда также тяжело мыться [в бане из-за жары]. (15) Псом (Canis) же она названа потому, что причиняет телам болезнь, или из-за яркости (candor) пламени, чтобы таким образом получилось, чтобы она казалась светящей впереди [=ярче] прочих. Она была названа Сириусом, потому что ее знали лучше [других звезд]594.
(16) Светила-кометы 595 (cometae) наречены так потому, что рассыпают за собою волосы (κόμαι) света. Когда появляется этот род звезд, он означает моровое поветрие или голод, или войну. (17) По-латыни же кометы именуются волосатыми, ибо они разбрасывают языки пламени в виде волос (crinia). Стоики говорят, что их [числом] за тридцать, их имена и действия записали некоторые астрологи.
(18) Светоносец (Lucifer) назван так потому, что среди прочих звезд несет больше света596. Это одна из планет. Ее справедливо именуют гривой (iubar) потому, что она распускает свет подобно гриве, но и сияние Солнца, Луны и звезд также именуется этим словом, поскольку они распространяют свои лучи в виде гривы597.
(19) Вечерняя звезда (Vesper) – западная, каковое прозвание она получила от Геспера598, царя Испании. Она же – и одна из пяти светилпланет, приводящая ночь и следующая за Солнцем. Говорят, что это светило на востоке является Светоносцем, а на западе – Вечернею звездою599. О чем Стаций:
В переменной среде единственный светоч родится
(Stat., Theb., VI, 241).
(20) Светила-планеты – это те, которые не закреплены на небе, как прочие, но носятся в воздухе. Названы же они планетами α=πὸ τη̂ς πλάνης, то есть «от блуждания». Ведь они носятся иногда на юге, иногда на севере, по большей части против [движения] мира [=сферы неба], и никогда – вместе с миром. Их греческие имена – Φαέθων, Φαίνων, Πυρίων, ʼˊΕσπερος, Στίλβων600. (21) Их римляне увековечили именами своих богов, то есть Юпитера, Сатурна, Марса, Венеры и Меркурия [соответственно]. Обманутые ведь и стремящиеся обманывать в своем раболепии, представляя себе что-то из-за любви, они показывали на небе звезды, говоря, что Юпитер есть та звезда, а Меркурий – эта: и возникло праздное мнение. Это ошибочное мнение укрепил диавол, а Христос опрокинул601.
(22) Далее же в тех [созвездиях], которые самими язычниками именуются «знаками», создается также и образ живых существ, как, [например,] Медведица, <как> Овен, Телец, Весы и тому подобные. Те же [люди], которые хорошо разобрались в созвездиях, побуждаемые пустым суеверием, поместили в число светил и [некий] вид тела, по каковым причинам они создали и образы, и имена своих богов.
(23) Ведь первый знак, Овен (Aries), который, как и Весы, говорят, [находится] на средней линии мира602, они называли из-за Амона-Юпитера потому что, на его голове, создавая призрачный образ (simulacrum) [этого бога], они выдумали бараньи рога603. (24) Этот знак язычники потому установили первым среди знаков, что, говорят, в марте месяце, который есть начало года [у римлян], Солнце направляет свой путь в этот знак.
(24) Но и самого Тельца (Taurus)604 среди созвездий помещают в честь Юпитера потому, что, согласно мифу, он превратился в быка, когда похитил Европу.
(25) Также Кастора и Поллукса, [говорят,] после смерти поместили среди созвездий: этот знак называют Близнецами (Gemini)605.
(26) Затем говорят о Раке (Cancer)606 потому, что когда к этому знаку Солнце приходит в месяце июне, оно начинает двигаться вспять на манер рака, делая дни короче. Неясно ведь, где у этого животного передняя сторона, то есть он направляет свой шаг в обе стороны, так как [у него] передняя сторона – это задняя, и задняя – это передняя.
(27) Огромного Льва (Leo)607 в Греции убил Геркулес, и он был помещен среди двенадцати знаков из-за своей мощи. Когда Солнце касается этого знака, оно отдает миру чрезмерно много тепла и производит ежегодные этесийские ветры.
(28) Знак же Девы (Virgo)608 был размещен среди звезд ввиду того, что в те дни, в которые Солнце движется по этому [знаку], выжженная солнечным жаром земля не рождает [плодов]. Ведь это время каникулярных дней.
(29) Весы (Libra)609 же названы так от равенства своего месяца, ибо в VIII день до октябрьских календ (24 сентября) Солнце, двигаясь в этом знаке, совершает равноденствие. Поэтому и Лукан [говорит]:
…По Весам времена уравнявши (Lucan., Phars., IV, 58).
(30) Скорпион (Scorpio, Scorpius)610 же и Стрелец (Sagittarius)611 названы так из-за молний в своих месяцах. Стрелец – это человек с ногами в форме лошадиных, которому добавили стрелы и лук, поскольку в его месяце были видны молнии. Потому и наречен Стрельцом.
(31) Знак Козерога (Capricornus)612 поместили среди звезд из-за козы613, кормилицы Юпитера. Ее задней части потому придали вид рыбы, что на те же времена [года] определяли дожди, которые в этом месяце преимущественно бывают наибольшей силы.
(32) Далее Водолей (Aquarius)614 и Рыба (Piscis)615 названы от времен дождей, потому что зимой, когда Солнце движется в этих знаках, проливаются более сильные дожди.
И удивительно безумие язычников, которые не только рыб, но даже баранов и козлов, и быков, и медведей, и собак, и раков, и скорпионов перенесли на небо! Ведь и Орла (Aquila), и Лебедя (Cignus)616 из-за басен о Юпитере они поместили среди небесных звезд, ради памяти о них!
(33) Также они поверили, что Персей (Perseus) и жена его, Андромеда (Andromeda)617, после своей смерти были взяты на небо, так как они показывали их образы среди звезд и не стыдились называть [звезды] их именами.
(34) Они поместили Возничего (Auriga)618 Эрихтония среди небесных звезд, потому что думали, что он первым составил квадригу. Ведь они были восхищены, что его гений дошел до уподобления Солнцу, и поэтому они поместили его имя после смерти среди созвездий.
(35) Так и Каллисто́, дочь царя Ликаона, будучи изнасилованной Юпитером, согласно басням, была превращена Юноною в медведицу, которая по-гречески называется α=᾿ ρκτος, и после ее убийства Юпитер перенес ее имя вместе с [именем ее] сына в созвездие Септентрионов. Ее саму он назвал Арктом, а ее сына – Медвежьим стражем.
(36) Так и Лира (Lyra)619 была размещена на небе из-за Меркурия.
Так и Кентавр (Centaurus)620 Хирон был зачислен в созвездия из-за того, что вскормил Эскулапа и Ахиллеса.
(37) Но из какого бы суеверия люди их не называли, они суть светила, которые Бог создал в начале мира и посредством определенных движений [которых] установил порядок отделения времен. (38) Наблюдения, следовательно, этих знаков или рождения [под ними], или прочие суеверия, которые связываются с постижением созвездий, то есть с узнаванием судеб, – [все они,] без сомнения, вере нашей противны, и должны быть так неведомы христианам, чтобы их даже в записи не видели. (39) Но некоторые, соблазненные красотою и лучезарностью звезд, из-за слепоты умов впали в ошибку в связи со светилами, – в такую, что посредством вредных вычислений, которые зовутся звездочетством (mathesis), они пытаются получить возможность предугадать судьбы вещей. Каковых [людей] не только ученые христианской религии, но даже и язычники Платон и Аристотель, и другие, подвигнутые истиною вещей, осудили согласным мнением, говоря, что от таких мнений рождается только смешение вещей. (40) Ибо, если бы род людей был предназначен к различным деяниям по необходимости рождения, почему [тогда] хорошие [люди] заслуживали бы похвалы, а дурные получали бы законную кару? И как бы они не предавались мудрствованию о небе, но заблуждения их опровергнуты свидетельством истины621.
(41) Порядок же этих вот семи светских наук потому философами был доведен вплоть до звезд [=астрономии], что души, конечно [еще] запутанные светскою мудростью, [уже] отвлекались от земных вещей, и поднимались к высшим созерцаниям.
* * *
Примечания
Μανθάνω – это по-гречески «учиться, узнавать, слышать». В дальнейшем за этим корнем все больше закрепляется значения не «учения» вообще, а учения о числах, количествах и величинах в частности. Поэтому у Платона и Аристотеля μαθηματική (подразумевается τέχνη) – «наука о величинах». Однако и старое значение сохранялось, то есть μαθηματικός могло означать просто «ученый».
Весь абзац дословно переписан из «Наставлений...» Кассиодора, кн. II, гл. «О математике», а тот воспроизводит рассуждения Боэция (Boet., Inst, arithm., 1,1). О первоочередности наук ср. Arist., An. post., I, 27: 87а.
Число. Греческая математика начала с наглядного представления о числе, то есть умственного образа некоторого количества, например счетных камушков (псефов). И впоследствии «число» для греков – всегда натуральное число. Остальные числа были для у них чем-то соотносительным: отрицательные числа они рассматривали как натуральные в позиции вычитаемого, а рациональные – как простую дробь двух натуральных (десятичные дроби в Европе были изобретены в XVI в. н. э.). Иррациональные числа представляли себе исключительно геометрически, например, как гипотенузы прямоугольных треугольников с соответствующими катетами.
Никомах из Герасы (перв. пол. II в. н. э.) – неопифагорейский философ и математик. Сохранились его работы «Введение в арифметику» и две книги «Теологуме нов арифметики», а также «Руководство по гармонике» (учебник пифагорейской теории музыки), «Введение в геометрию» (не сохранилась), «Жизнь Пифагора». «Теологумены...» были посвящены символике, мистике чисел и отчасти «философии числа»; в своих философских взглядах придерживался поздней платонической доктрины, а также некоторых идей Филолая из Кротона (V в.). «Введение в арифметику» было введением в пифагорейскую математику, извлеченную, в основном, из Евклида с привлечением сохранившихся работ Архита. Доказательств теорем не приводится, так как работа писалась для широкой публики. И хотя учебник апеллировал к достижениям науки 600-летней давности, он из-за своей простоты пользовался популярностью; свои комментарии к нему оставили неоплатоники Ямвлих Халкидский (кон. III в. н. э.) и Иоанн Филопон (VI в. н. э.). Переведено на латынь Апулеем (перевод не сохранился) и Боэцием.
Для Исидора практически единственным источником по данному титулу и началу следующего является трактат Аврелия Кассиодора (VI в. н. э.) «Наставления в науках божественных и светских» (кн. II, титул 4: De arithmetica), который делает кратчайшую выжимку из двух книг Боэция «О наставлении в арифметике» («De institutione arithmetica»), которые, в свою очередь, являются адаптированным переводом «Введения в арифметику» Никомаха. Этим и объясняется набор упоминаемых имен. Вообще математические науки не принадлежали к сфере интересов Исидора Севильского (в отличие от дисциплин «тривиума» и натурфилософии), поэтому он и опустился до почти дословного цитирования Кассиодора.
Это заявление – остаток пифагорейской и неопифагорейской онтологии. Дело в том, что пифагорейские (возможно) и неопифагорейские философы считали, что единица (монада) – бог и начало всех вещей в мире. Это как бы всеобъемлющее единство, целостность, определенность, посредством которой можно различить все вещи и все сосчитать. Двойка (диада) тоже не была числом и символизировала беспредельность, так как через две точки можно провести бесконечную прямую. Сама по себе беспредельность – это плохо, поскольку ее невозможно охватить мыслью. Первым числом была тройка (триада), как единство предела и беспредельности. По крайней мере, так мы сегодня пытаемся совместить рассказы о Филолае Кротонском (V в.), авторе пифагорейской «философии числа», будто он, с одной стороны, считал началом монаду (по Ямвлиху), а с другой стороны – предел и беспредельное (по Стобею, а также Аристотелю, если считать, что учение упомянутых у последнего «анонимных пифагорейцев» – это учение Филолая в части «философии числа»; см. Arist., Met., I, 5: 986а 13). Восстановить подлинную онтологию пифагорейских философов (самого Пифагора, Алкмеона, Филолая) достаточно сложно ввиду немногочисленности и противоречивости сохранившихся фрагментов, зато неопифагорейцы (Нумений, Модерат, Никомах) выражались более определенно. Например, Никомах пишет, что бог тождественен монаде, «ибо он является семенным началом всех вещей в природе, включающим в себя числа и потенциально охватывающим все вещи, которые проявляются как крайние противоположности», тогда как диаду он считал первичной неоформленной материей. Тут, конечно, чувствуется влияние и физики стоиков с их «семенными логосами». Мистика чисел встречается на латинском языке в комментарии неоплатоника Макробия на «Сон Сципиона». Разумеется, такова была позиция философов: профессиональные математики, не мудрствуя лукаво, полагали числами и единицу, и двойку.
Единица ведь получила имя от греческого языка. Количественные числительные до ста единообразны во всех индоевропейских языках, то есть происходят от общего праязыка. Для примера приведем числительные из санскрита: 1 – «э́ка», 2 – «два», 3 – «три», 4 – «чату́р», 5 – «па́нча», 6 – «шаш», 7 – «сапта́», 8 – «ашта́», 9 – «на́ва», 10 – «да́ща», 20 – «винчати́», 30 – «тринча́т», …, 100 – «щата́», 200 – «две щате́». Некоторое время вызывал разноречивые мнения вопрос от том, какой согласный стоял в индоевропейском праязыке вначале числительных 4 и 5, если он смог превратиться и в губной «п», и в передненёбный аффрикат «ч», и в переднеязычный «т», и в заднеязычный «к». Сегодня полагают, что латынь дольше всех сохранила старое звучание этого согласного, который записывается как «к у̌
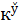
».
Тысяча, которую греки называют μυριάς. Исидор ошибается, по-гречески мириада – это 10 000.
Ci.: habere вм. habent.
Шестерка, совершенная в своих частях – так как 6 == 1 2 3. О совершенных числах см. ниже гл. 5, §11 и примечание к нему.
Время возвращающегося года. Это эналлага: имеется в виду (постоянно) возвращающееся время года.
Эта теория принадлежит к самому древнему пласту пифагорейской арифметики, скорее всего, Пифагору лично, и к началу IV в. уже отошла на задний план, продолжая играть роль элементарного введения в арифметику для непрофессионалов (почему к теме четных и нечетных чисел так часто обращаются и Платон, и Аристотель). После трудов Евдокса Книдского (рубеж IV-III вв.) она стала уже некоторым математическим раритетом, не имеющим прямой связи с современною арифметикою.
2, 4, 8. В латинской редакции Линдсея римские цифры и словесно выраженные числительные употребляются без различия (в рукописях – то же самое, но в еще большей степени). Чтобы передать дух этой несогласованности, мы оставляем в переводе римские цифры такими, какими они являются в тексте. Кроме того, различия в правописании словесных числительных мы передаем так: латинские количественные числительные (unum, duo, tres, quattuor и т. д.) переводятся такими же русскими числительными (один, два, три, четыре и т. д.); порядковые числительные – как русские порядковые; числительные кратности (singuli, bibi, terni, quaterni, quini и т. д.) – как «по одному», «по два», «по три», «по четыре», «по пять» и т. д.; прилагательные кратности (unitas, binarius, ternarius, quaternaries, quinarius, senarius и т. д., – подразумевается numerus) переводятся как «единица», «двойка», «тройка», «четверка», «пятерка», «шестерка» и т д., поскольку термины «двоичное», «троичное» [число] и т. п. сегодня используются для обозначения систем счисления; наречия кратности (semel, bis, ter, quarter, quinquies и т. д.) – как «один раз», «два раза», «три раза», «четыре раза» и т. д. Греческие термины, как обычно, оставляются по-гречески, a unitas переводится по-разному в зависимости от контекста.
Нечетные числа 3, 5, 7, 9 и прочие. Заметим, что единица (монада) считалась не нечетным числом, а четным и нечетным одновременно, так как порождала оба вида числа (см. Alex. Aphrodis., Comm, in Met. I, 5: 985b23). To есть для нечетных чисел принималась формула 2n1, n ∈
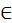
N.
Измеряться каким-либо числом – иметь его своим делителем. То есть нечетно-нечетные числа – произведения нечетных чисел; их формула: (2nl)(2kl), где k, n ∈
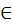
N. Правда, Исидор свои примеры почему-то ограничивает квадратами нечетных чисел.
Простые числа – такие, которые не имеют никакого другого делителя, кроме одной целой. Мы бы сказали: «кроме единицы и самого себя». Кассиодор говорит: «которые измеряются одной единичной мерой (sola monadica mensura)», что и означает кратность себе и единице. Однако Исидор вводит здесь одно усложнение, так как полагает, что, например, 1/5 есть делитель 5 (конечно, он имеет в виду 1/5 от 5, то есть 1), 1/3 – делитель 3 и т. д. По сегодняшним понятиям, 1 и 2 также относятся к простым числам. Теория простых чисел – один из самых увлекательных разделов арифметики. Ею занимались Евклид, доказывавший что таких чисел бесконечно много, Эратосфен, предложивший простой метод «отсеивания» составных чисел до любого наперед заданного («решето Эратосфена»), П. Ферма и М. Мерсенн, безуспешно искавшие формулу для простых чисел и исследовавшие некоторые разновидности этих чисел (например, простые числа Мерсенна вида 2 n
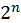
–1), Л. Эйлер, обобщивший всю теорию простых чисел. А. Лежандр, К. Гаусс, Л. Дирихле, Ж. Бертран, П. Л. Чебышев, Ж. Адамар и многие другие занимались вопросом о том, как простые числа распределяются среди натуральных чисел. Например, удалось показать, что π(n) ≈
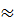
n/In n, где π(n) – количество простых чисел, не превосходящих п. (См. Серпинский В. Что мы знаем и чего мы не знаем о простых числах. – М.: Физматгиз, 1963.)
И снова Исидор выражается менее ясно, чем Кассиодор, который правильно говорит, что составные числа – те, которые [нацело] делятся как на единицу (или себя), так и на другое число.
Средние числа – такие, которые, кажется, некоторым образом являются простыми и несоставными, а другим образом – составными. Имеются в виду простые дроби, которые могут быть и несокращаемыми и сокращаемыми. Несократимую же дробь пифагорейцы называли питменом (πυθμήν).
Совершенным называется число, равное сумме своих делителей, исключая его самого. Ниже Исидор перечисляет три первых совершенных числа – 6, 28 и 496. Четвертым будет 8218, а восьмое, например, имеет порядок 10 24
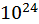
. Эмпирическую формулу для совершенных чисел вывел Евклид: 2 n ( 2 n1 –1)
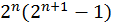
, где n ∈
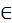
N, но число 2 n1 –1
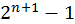
должно быть простым (так называемое, простое число Мерсенна). То есть, например, для первых одиннадцати совершенных чисел n == 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 127. Впоследствии Л. Эйлер доказал, что этой формулой исчерпываются все четные совершенные числа. Однако, вопреки заявлению Исидора, вопрос о том, являются ли все совершенные числа четными, до сих пор открытый. В XX в. удалось доказать только то, что если нечетные совершенные числа и существуют, то они должны делиться по крайней мере на пять различных простых чисел и должны быть чрезвычайно большими, так как проверены все числа до 1050. Неизвестно даже, есть ли совершенным числам предел или их бесконечно много: сегодня известно более тридцати, и последнее имеет n == 132050. Раздел, посвященный этим числам, – один из интересных разделов арифметики.
Общее примечание к главе 5. О первом разделении чисел на четные и нечетные. К Пифагоровой теории четных и нечетных чисел относилось, по словам Ямвлиха (в которых в данном случае нет оснований сомневаться), также открытие так называемых «дружественных чисел», то есть таких, каждое из которых равно сумме делителей другого числа, например 220 и 284 или 2620 и 2924.
Число по отношению к другому. Заметим, что здесь и далее Исидор и его неопифагорейский источник допускают двусмысленность. Говоря об отношении двух чисел, он имеет в виду как собственно некое отношение, тип связи двух чисел (больше, меньше, равно, отношение двухкратности, отношение суперпартикулярности и т. п.), так и простую дробь (5/3, 3/5, 2/2, 2/1, 3/2 и т. п.), которая в нашем сегодняшнем понимании есть одно рациональное число (1,6(6); 0,6; 1; 2; 1,5 и т. п.). Исидор, равно как и ранние пифагорейцы, не различал этих ситуаций. Вообще учение о пропорциях разрабатывалось не в связи с арифметикой, а в связи с гармоникой, то есть в связи с поисками консонансов и диссонансов струн разной длины (октава – отношение 2/1, квинта – 3/2, кварта – 4/3, большая и малая терции – 5/4 и 6/5 соответственно) потому чаще встречается у теоретиков музыки, пифагорейских и других. Боэций данные определения отношений помещает как в свой музыкальный трактат, так и в арифметический. Исидор следует Флавию Кассиодору. Вся дальнейшая теория будет связана с анализом отношения чисел p и q, p=nqm, где p, q, n ∈
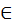
N, m ∈
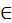
Z при произвольном q и различных значениях параметров m и n. А именно: при n=1, m=0 – равенство, при n=1, m ≥
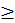
1 (или n ≥

2, m>q(1–n))-р больше q, в частности для отношения р к q, при n ≥
2, m=0 – многократность, при n=1, m=1 – суперпартикулярность, при n=1, m ≥
2 – суперпартиентность, при n ≥
2, m=1 – многократная суперпартикулярность, при n ≥
2, m ≥
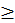
2– многократная суперпартиентность. Отношения меньше, подмножителя, субсуперпартикулярности, субсуперпартиентности, многократной субсуперпартикулярности и многократной субсуперпартиентности – это обратные предыдущим шести, то есть такие, в которых при тех же значениях параметров рассматривается не отношение р к q, а отношение q к р, где р=nqm. Данное исследование принадлежит поздним пифагорейским математикам, скорее всего, Архиту, хотя начальная часть этой теории (до суперпартикулярности включительно) восходит к Пифагору.
Число р называется суперпартикулярным по отношению к q, если p=q1, где p, q ∈

N. Соответственно отношение суперпартикулярности – это отношение вида (q1)/q=1 1/q
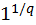
. Для q=1 суперпартикулярность становится многократностью (двухкратностью). В этом и последующем определении под дополнительной «одной частью» будет иметься в виду 1/р-тая часть числа р, то есть просто единица, аналогично «две части» – двойка и т. д.
Число р называется суперпартиентным по отношению к q, если p=qm, где р, q, m ∈
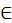
N, m ≥
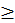
2. Соответственно отношение суперпартиентности – это отношение вида (qm)/q=1 m/q
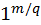
. Для m=kq, k ∈
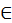
N суперпартиентность становится многократностью.
Число q называется субсуперпартиентным по отношению к р, если р=qm, где p, q, m ∈
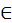
N, m ≥
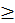
2. Соответственно отношение субсуперпартиентности – это отношение вида q/(qm). Для m=kq, k ∈
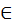
N субсуперпартиентное число становится подмножителем.
Число q называется субсуперпартикулярным по отношению к р, если р=q1, где p, q ∈

N. Соответственно отношение субсуперпартикулярности – это отношение вида q/(q1). Для q=1 субсуперпартикулярное число становится подмножителем (половиною).
Число р называется многократно суперпартикулярным по отношению к q, если p=nq1, где p, q, n ∈
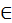
N, n ≥

2. Соответственно отношение многократной суперпартикулярности – это отношение вида (nql)/q=n 1/q
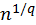
.
Число q называется многократно субсуперпартикулярным по отношению к р, если p=nq1, где p, q, n ∈
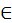
N, n ≥
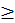
2. Соответственно отношение многократной субсуперпартикулярности – это отношение вида q/(nq1).
Число р называется многократно суперпартиентным по отношению к q, если р=nqm, где p, q, n, m ∈
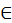
N, n ≥
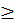
2, m ≥
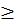
2. Соответственно отношение многократной суперпартиентности – это отношение вида (nqm)/q=n m/q
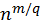
. Для m=kq, k ∈
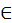
N многократная суперпартиентность становится многократностью. Для m=kq1, k ∈
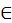
N многократная суперпартиентность становится многократной суперпартикулярностью. Если снять условие n ≥
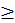
2, то многократная суперпартиентность становится простою суперпартиентностью. Если снять условия n ≥
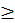
2, m≥
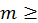
2, то многократная суперпартиентность становится простою суперпартикулярностью.
Ci.: subsuperpartionalis вм. superpartionalis.
Число q называется многократно субсуперпартиентным по отношению к р, если р=nqm, где p, q, n, m ∈
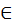
N, n ≥
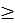
2, m≥
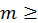
2. Соответственно отношение многократной субсуперпартиентности – это отношение вида q/(nqm). Для m=kq, k ∈
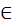
N многократно субсуперпартиентное число становится подмножителем. Для m=kql, k ∈
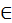
N многократная субсуперпартиентность становится многократной субсуперпартикулярностью. Если снять условие n ≥
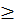
2, то многократная субсуперпартиентность становится простою субсуперпартиентностью. Если снять условия n ≥
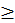
2, m ≥
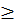
2, то многократная субсуперпартиентность становится простою субсуперпартикулярностью.
Линейные, плоскостные и объемные числа. Теория фигурных (геометрических) чисел также восходит к раннепифагорейской традиции. Считая числа при помощи камешков-псефов, математики обращали внимание на те случаи, когда эти камешки можно было сложить в виде правильной фигуры. Кроме пифагорейцев, трактаты «О многоугольных числах» оставили Гипсикл (II в.) и Диофант (II в. н. э.), причем часть сочинения последнего сохранилась. Из математиков более поздних времен, этими числами увлекались П. Ферма и Б. Паскаль. Наиболее известными были треугольные, квадратные, пятиугольные, пирамидальные и кубические числа. N-e треугольное число, как легко заметить, представляет собою сумму чисел арифметической прогрессии, у которой первый член – единица и разность также единица, поэтому его формула проста: n(n1)/2. Если обобщать на общий случай арифметической прогрессии, то следовало бы говорить о трапецеидальных числах (трапеция получится косоугольной).

Квадратные и кубические числа – очевидно просто квадраты и кубы натуральных чисел; их формулы для n-го числа соотвественно:n 2
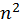
и n 3
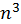
:

Пятиугольные числа немного сложнее. Чтобы посчитать n-е пятиугольное число, его надо разбить на два треугольных, после чего останется еще л точек с краю. Формула получается такая: nЗn(n–1)/2.

Подобным образом можно образовывать любые многоугольные числа. Формула для n-го k-угольного числа такова: n(k–2)n(n–1)/2. Иногда выделяют еще прямоугольные числа, то есть составные, поскольку любое составное число можно, очевидно, выложить в виде прямоугольника со сторонами больше единицы. N-e пирамидальное число, как нетрудно заметить, равно сумме всех треугольных чисел от первого до л-го. Формула для вычисления такого числа имеет вид: n(n1)(n2)/6.

Непрерывное число – это когда число понимают как единицу длины.
Квадратные числа оказываются весьма интересными, так как при исследовании их свойств, вероятно, пифагорейцами был получен метод определения «Пифагоровых» или «вавилонских» чисел – целочисленных длин катетов и гипотенузы любого прямоугольного треугольника, то есть решению в целых числах уравнения X 2
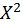
Y 2
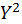
==Z 2
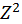
. Дело в том, что переход от одного квадратного числа к другому осуществлялся с помощью гномона – наращения в виде уголка чисел-псефов с двух сторон квадрата. Например, нижеследующее квадратное число получено с помощью пяти гномонов:
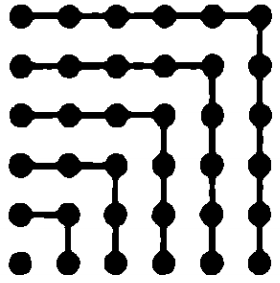
Ставится задача: если гномон – квадратное число, то какому правилу должно отвечать квадратное число, полученное с его помощью, ведь тогда получится, что квадратное число плюс квадратное число дает квадратное число. Легко заметить, что, если Х – квадратный гномон, то предыдущее квадратное число – (X 2
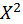
–1)/2, а последующее – (X 2
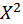
1)/2 (поскольку гномон всегда равен 2Y1, где Y – сторона предыдущего квадрата), где X – нечетное число. Правда, такое решение является частным случаем общей формулы Пифагоровых троек, так как в нем есть дополнительное условие: Z=Y1, то есть чтобы катет и гипотенуза были бы двумя соседними квадратными числами. Общее решение см., например, в «Началах» Евклида, кн. X, предл. 29, или в «Арифметике» Диофанта, кн. II, задача 8 (та самая, к которой П. Ферма сделал свое знаменитое замечание на полях).
Циклические и сферические числа (см. ниже) имеют не столько геометрическую, сколько арифметическую интерпретацию: это степени чисел 5 и 6, которые, как известно, кончаются всегда также на 5 и 6, то есть «возвращаются к себе», говоря словами Кассиодора и Исидора, – и в этом смысле они подобны кругам. Иначе говоря, циклическое число – такое, квадрат которого оканчивается на те же цифры, из которых состоит оно само (например, 25 и 25x25=625), а сферическое число – такое, квадрат и куб которого оканчивается на те же цифры, из которых состоит оно само (например, 6, 6x6=36 и 6x6x6=216).
Пирамида – поднимающееся пламя. Имеется в виду греческая этимология слова «пирамида» от πυ̂ρ (огонь, пламя).
Глава 8. О различии арифметики, геометрии и музыки. Название главы крайне неудачно: ее следовало бы озаглавить «О различии среднего арифметического, среднего геометрического и среднего гармонического», ибо речь пойдет именно об этих трех средних. Кстати, все три пропорции, по вполне достоверному преданию, были известны опять-таки самому Пифагору, причем Ямвлих приписывает ему также изобретение «музыкальной пропорции» (см. ниже). Наш автор ничего не пишет о знаменитом неравенстве средних: c h ≤ c g ≤ c m
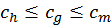
, хотя оно было хорошо известно древним, так как очевидно вытекало из геометрического построения всех трех средних величин (см., например в «Математическом собрании» Паппа Александрийского).
В арифметике среднее ты ищешь так. Речь о среднем арифметическом двух чисел а и b – числе c m
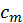
==(аb)/2. Обобщенно – средним арифметическим n положительных чисел a 1
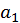
, a 2
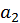
, …, a n
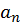
называется число c m
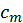
== (a 1
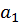
a 2
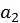
…a n
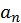
)/n. Оно потому называется арифметическим, что если не искать среднего между четным и нечетным числом (чего делать не рекомендовалось), такая операция не выводит за пределы множества натуральных чисел (объекта арифметики).
При помощи же геометрии так ищешь среднее. Среднее геометрическое двух чисел а и b – это число c g = ab
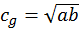
. В общем случае – средним геометрическим n положительных чисел a 1
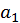
, a 2
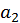
, …, a n
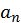
называется число c k = n a 1 a 2…a n
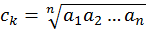
Для 6 и 9 среднее геометрическое – иррациональное число 72
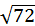
==8,4853... Исидор знает иррациональные числа только как геометрические фигуры (см. главу 11, §3), поэтому средних геометрических у него не одно, а два. То есть ищутся два наиболее близких по величине делителя числа ab: в данном случае 8 и 9. Два средних геометрических – это результат позднейшей арифметизации математики. Во времена Евклида среднее геометрическое было одним числом, представляемым в виде отрезка на специальном чертеже.
Исидор пишет: «quot media duplicata» – «дважды умноженные средние»
При помощи музыки так... Среднее гармоническое двух чисел а и b – это число c h
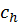
==2ab/(ab). В общем случае – средним гармоническим n положительных чисел a 1
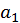
, a 2
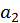
, …, a n
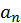
называется число c h =n/( 1 a 1 1 a 2 … 1 a n )

. Исидор определяет среднее гармоническое через пропорцию: (c h
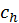
–a):a=(b–c h
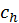
):b. Пример Исидора также звучит темно: «Utputa VI et VIII; duabus partibus superant, quae duae partes tertia media, octo, superatur ab ultima попа». Мы предлагаем такую реконструкцию: 4...quae duae partes [duodenarii sunt] tertia media, [id est] octo, [quae (media)] superatur ab ultima попа», полагая, что под «третьим средним» имеется в виду среднее гармоническое, третье после арифметического и геометрического. Кроме того, девятка могла возникнуть еще и в связи с «музыкальной пропорцией»: äc h

==c m
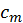
:b, то есть 6:8=9:12. Вычисления здесь могли быть такими: 8–6=2=6x2/6; 12–9=3=9х2/6. Если бы в конце стояло не 9, а 12, то перевод был бы проще: «[восемь] превосходит [шесть] на две [шестых] части, и на эти же две [шестых] части [от 12], треть, восьмерка превосходится крайними 12-ю. (См. также гл. 23.)
Сложно сказать, кому из математиков первому пришла в голову эта мысль (Архимед приписывает ее Евдоксу), но ее блестящее изложение читатель может найти в «Псаммите» Архимеда (см. Архимед. Сочинения / Пер. и комм. И. Н. Веселовского. – М., Физматгиз, 1962).
...Каковые суть у Платона числом пять. Исидор, очевидно, путает пять правильных многогранников, о которых говорит Платон в «Тимее» (Plat., Tim., 53с-55с), с пятью видами плоских фигур (см. ниже, гл. 12, §§1–2).
Телесные фигуры – это те, которые содержатся в длине, ширине и высоте. На данном месте у Кассиодора кончается содержательная часть (Cass., Inst., II, 6), поэтому все дальнейшее взято Исидором из другого, неизвестного нам, источника. По всей вероятности, им был утраченный еще в раннем средневековье трактат Боэция о геометрии. Впоследствии под его именем ходили два геометрических трактата, пятикнижный и двухкнижный, но оба подложные. Правда, можно предположить, что оригинальный текст Боэция вошел частично и в тот и в другой.
Телесные фигуры... разновидностей коих на плоскости пять. (Figurae solidae sunt, quae longitudine, latitudine et altitudine continentur, ut est cubus, cuius species quinque in piano.) Место, испорченное в рукописи. Вся фраза, начиная с «Figurae solidae...» (Телесные фигуры...), помещена в начало главы 12, но определение объемных фигур явно должно относиться к главе И. Непонятно, хочет ли Исидор сказать здесь, что существует пять твердых (solidae) фигур на плоскости, или, завершив определение объемных фигур и проиллюстрировав это определение кубом, он желает теперь перейти к детальному рассмотрению плоских фигур, упомянутых в гл. 11, §2. Второе вероятнее, поэтому мы предлагаем читателю вариант, в котором заголовок главы 12 разбивает предложение так, что «cuius species...» (разновидностей коих...) относится к геометрическим фигурам вообще.
В тексте издания Линдсея рисунки отсутствуют, в рукописи – тоже, хотя для них оставлено много пустого места. Поэтому рисунки приведены по изданию Ф. Аревало, который пишет, что нашел их в первом издании «Этимологий» (без года и места издания). Нужно иметь в виду, что рис. 4–5 изображают треугольники очень неточно: из них первый должен быть прямоугольным, а второй – равносторонним. Мы оставляем все как есть, включая грамматические ошибки, чтобы показать, с какими трудностями реально сталкивался при чтении Исидора средневековый читатель.
Четырехсторонняя фигура – это квадрат. Здесь Исидор смешивает род геометрической фигуры, а именно четырехугольник, с ее частным случаем – квадратом.
Διὰ α=ναθετω̂ν γραμμω̂ν – доcл. греч. «между поставленными чертами». Сегодня мы знаем минимум шесть видов четырехугольников: правильный четырехугольник (квадрат), ромб, прямоугольник, параллелограмм, трапецию и неправильный четырехугольник; Исидор знал два, причем уже невозможно понять, где он усматривал различия между «четырехсторонней фигурой» и «фигурой διὰ α=ναθετω̂ν γραμμω̂ν». Нелепое пояснение, что «четырехсторонняя фигура» есть квадратная и позднейший рисунок, изображающий «фигуру διὰ α=ναθετω̂ν γραμμω̂ν» в виде прямоугольника, только ухудшают ясность. Может быть, имелось в виду, напротив, что «квадрат – это четырехсторонняя фигура», а «фигура διὰ α=ναθετω̂ν γραμμω̂ν» – прямоугольник или параллелограмм, или трапеция, а может быть, Исидор просто не понимал, что писал. Аревало дает конъектуру dia catheton grammon («между косых черт»), то есть это та же трапеция.
Греч.: ο=ρθογώνιον (подразумевается τρίγωνον – треугольник). Кажется, Исидор смешивает прямой угол и прямоугольный треугольник, делая ту же ошибку, что и с четырехугольником.
̓ Ισόπλευρον (подразумевается τρίγωνον) – греч. «равносторонний треугольник». Текст Исидора не вполне ясен: Isopleuros figura plana, recta et subter constituta. Вероятно, «subter constituta» – это ссылка на рисунок, который должен был в рукописи следовать ниже.
Куб – это собственно телесная фигура, которая содержится в длине, ширине и высоте. Такое определение, конечно, не дает возможность отличить куб от прочих тел. Для примера приведем определение Евклида: «Куб – это объемная фигура, состоящая из шести равных квадратов» (Eucl., Elem., XIII, 25).
Цилиндр – это квадратная фигура, имеющая сверху полукруг. Откуда Исидор взял это невероятное определение или как он сам до него дошел, остается тайной. Возможно, это описание двухмерного изображения цилиндра (см. рис. 8). Евклид определяет цилиндр как фигуру вращения: «Когда одна из сторон... прямоугольного параллелограмма остается на месте, а сам параллелограмм поворачивается вокруг и возвращается в положение, откуда его начали двигать, получается фигура цилиндр» (Eucl., Elem., XI, 21).
Конус – это фигура, которая сужается от широкого основания, как прямоугольный треугольник. Ср. определение Евклида: «Когда одна из сторон, находящихся у прямого угла в прямоугольном треугольнике, остается на месте, а сам треугольник поворачивается вокруг и возвращается в положение, откуда его начали двигать, получается фигура конус» (Eucl., Elem., XIII, 18). «Определение» Исидора, возможно, просто описывает двухмерное изображение конуса.
Пирамида – это фигура, которая остро сходится от широкого основания. У Евклида: «Пирамида – это фигура, состоящая из плоских фигур, строящихся на одной плоской фигуре и сходящихся в точку» (Eucl., Elem., XIII, 12). Пирамида, конечно, не обязана иметь непременно острый угол при вершине, если только «острым» у Исидора не считается всякий угол. Но есть вероятность, что здесь под пирамидой имеется в виду тетраэдр, поскольку в V в. именно так он и назывался, а термин «тетраэдр» был придуман Героном, то есть спустя целых 400 лет после открытия самого этого правильного многогранника; сведения Исидора так или иначе восходят к Никомаху, а неопифагорейцы известны нарочитой архаизацией терминологии.
Ci. intra вм. infra.
Любое число есть в 10. Это заявление объясняется отчасти употребляющейся у греков системой счисления, в которой числа до 10 включительно записывались одним знаком («цифрой»), а с 11 – двумя и более знаками (исключая кратные 10,100, 1000), отчасти пифагорейскими источниками Исидора. Действительно, у пифагорейцев 10 было «совершенным числом», причем Никомах в «Теологуменах арифметики» (Nic., Theol. аr., 82, 10) приводит обширную цитату из популярной книжки платоника Спевсиппа «О пифагорейских числах» (переложение Филолая), вторая часть которой была посвящена различным уникальным свойствам десятки.
Внутри этого круга содержатся контуры всех фигур. Напомним, сегодня мы говорим, что описать окружность (сферу) вокруг какой-либо фигуры, означает найти такую окружность (сферу), на которой лежали бы все углы данной фигуры. Также это понимали и греки. Заметим, что вокруг всех вышеназванных плоских фигур могут быть описаны окружности, если под четырехугольником понимать прямоугольник. Для объемных тел, однако, следовало бы сказать «сфера», причем не вокруг всех пирамид и конусов можно описать сферы, и для конуса вписание в сферу имеет иной смысл. Правда, у нас нет уверенности, что Исидор понимал это именно так. Возможно, он просто имел в виду, что любую фигуру можно заключить в окружность (сферу) достаточно большого радиуса.
Границы повершостей – это линии, очертания которгях потому не были установлены среди десяти вышеназванных фигур, что они находятся среди них. (Superficiei vero fines lineae sunt, quorum formae ideo in superioribus decern figuris positae non sunt, quia inter eas inveniuntur.) Место неясное. To ли эти контуры не были упомянуты, потому что они вписываются в окружность («содержатся внутри круга»), как было сказано чуть выше, то ли имеется в виду, что границы фигур содержатся в самих фигурах, как, скажем, окружность – в круге, и поэтому о них нет смысла говорить отдельно. Второе вероятнее.
При помощи же геометрии так ищешь среднее число. См. примечание к гл. 8, §2. Оно называется геометрическим потому, что дает, главным образом, иррациональные числа, которые могли изучаться только в геометрическом представлении.
Общее замечание к Главе 14. Вся эта глава помечена у Линдсея как позднейшая вставка. В самом деле, она выглядит как отдельные комментарии, прежде бывшие на полях и перенесенные в конец титула. Первая часть главы, §§1–2, присутствует в Поблетской рукописи – она посвящена значению фигур в астрологии, поэтому мы позволили употребить здесь несколько современных астрологических терминов (Ср.: Ptol., Tetr., I, 13–16). Вторая часть, §§3–5, касается космического семичлена (см. ниже), однако в середине помещены два не связанных с этой темой фрагмента о совершенстве числа био том, что 9х6=54. Конец текста испорчен.
Объем, то есть тело, больше чего открыть невозможно. То есть невозможно представить себе что-то имеющее большую размерность, чем 3. Четырехмерной (и вообще л-мерной) геометрией математики занялись только в XIX в.
Здесь таким образом находятся два куба, то есть два тела. Непонятно, о чем речь. Во всяком случае, ничего из сказанного выше не имеет отношения к классической задаче удвоения куба. Сама задача была решена Менэхмом (сер. IV в.).
См. гл. 5, §11 и примечание к этому месту.
Inter primum in ordine, id est X, qui propter primum perfectum numerum cum primo versu multiplicans sexies noveni, LIV; novies seni, LIV. В этом месте, очевидно, лакуна и вообще текст испорчен. Предположительно, его можно восстановить так: «Между первым по порядку числом (8) и 10 есть число, то есть 9, которое...».
То, что материя имеет такое количество частей, познается по справедливости двумя [пропорциями?], из которых она имеет одну в таком порядке: 1,2,3, 4,9, 8, и вместе с ними 27. Весь этот чрезвычайно темный фрагмент восходит к Филолаю и его сочинению «О ритмах и мерах» то ли через «Гармонику» Никомаха и «Наставление в музыке» Боэция (Boet., Inst, mus., III, 5–8), толи через «Тимей» Платона (Plat., Tim., 35b-36b) и перевод Халкидия (см. также комментарии А. А. Тахо-Годи к этому месту «Тимея»). То есть имеется в виду, что материя космоса (у Платона – душа космоса) устроена по принципу пифагорейской, в частности филолаевской, музыкальной гармонии. Кроме того, космический семичлен (1, 2, 3, 4, 8, 9, 27) соотносился со светилами (Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн соответственно), что отчасти оправдывает помещение этого фрагмента в данную главу, поскольку она начинается с мысли, что светила придают иной смысл геометрическим фигурам и числам.
Музы же названы α=πὸ του̂ μάσαι. Конъектура Аревало: μω̂σθαι со ссылкой на платоновского «Кратила»: 4Музы и вообще мусические искусства названы... от страстного стремления (μω̂σθαι) к философской мудрости» (Plat., Crat., 406а). Однако перевод Исидора отвечает именно глаголу μάσαι.
Звуки... не могут быть записаны. Система нотации во времена античности существовала, и Исидор, конечно, об этом знал. Его замечание касается отсутствия звукозаписывающей и звуковоспроизводящей аппаратуры. В наиболее совершенной форме система греческой нотации описана у Гауденция («Введение в гармонику», III в. н. э.); она воспроизведена у Боэция в 4-й книге его музыкального трактата. Нотация была буквенной, то есть каждой струне двухоктавного диапазона в каждом из ладов присваивались обозначения (частично перекрывавшиеся), заимствованные из греческого и финикийского языков или придуманные специально. Метрические характеристики мелодии практически не отмечались, так как они были связаны с размером стихов, которые при этом напевались: трохеем, ямбом, дактилем и т. д. (см. кн. I, гл. 17). Уже после Исидора, в XIII в. н. э., появились знаки так называемой «мензуральной нотации», а с XVI в. для записи музыки употребляются привычные нам ноты.
Ci.: Iubal вм. Tubal
Пифагор изобрел начала этого искусства от звона молотков и бряцания на вытянутых струнах. Виновником этой легенды был Никомах из Герасы, который написал, будто Пифагор, проходя мимо кузницы, услышал звуки молотков и распознал в них октаву, кварту и квинту. Придя домой, он будто бы провел серию экспериментов с молотками, установил, что разница в тонах зависит от веса молотка, затем прикрепил к четырем струнам грузы, пропорциональные этим весам, и получил эти октаву, кварту и квинту. Этот псевдоэксперимент был опровергнут в XVI в., и, как остроумно заметил Й. Растед, своим возникновением он обязан ошибке автора или переписчика того источника, которым пользовался Никомах: вместо acpatpa (металлический шар или диск, с которым действительно иногда экспериментировали пифагорейцы) было написано acpupa (молоток). Остальные детали легенды домыслил сам Никомах. Правильное описание этого опыта дает Птолемей.
Лин, Зет и Амфион – мифические персонажи. Амфион, сын Зевса и Антиопы, увлеченно занимался музыкой, и под звуки его кифары сами укладывались камни стен города Фивы (Зет, его брат, был охотником). Лин, сын Гермеса и музы Урании, был поэтом, автором космогонии, по Диодору, – изобретателем ритма и мелодии (Diod. Sic., III, 67,1–4).
Глава 18. О трех частях музыки. Эта глава целиком взята из Кассиодора (Cass., Inst., II, 5, 5). В предыдущих главах также несколько фраз заимствованы из того же 5-го капитула II книги «Установлений...». Однако дальше Кассиодор уходит, в основном, в математическую теорию консонансов и ладов, а Исидор, хотя и основывается на том же источнике, то есть трактате Боэция, после изложения консонансов, предпочитает практическую часть – рассуждение о хореографии и различных музыкальных инструментах. Этим и объясняется тот факт, что дальше будет предложено тоже трехчастное, но несколько иное деление музыки.
Проще говоря, гармоника – это хореография, органика – наука о духовых инструментах, а ритмика – об ударных. Любопытно, что струнные щипковые инструменты (лира, кифара, форминга) помещаются в ту же группу, что и ударные (кимвалы, тимпаны).
Ci.: Cantorum вм. canorum
Голос есть воздух, колеблемый дыханием, от чего и наречены глаголы. См. кн. I, гл. 9, §1, и примечание к этому месту. Вообще звук в древности считался совокупностью следующих друг за другом «толчков» воздуха, при этом предполагалось, что, чем звук выше, тем он распространяется быстрее. Например, так полагал Архит (Porph., In Ptolem. Harm., 56During).
Созвучия. Они делятся на консонансы (созвучия в узком смысле) и диссонансы (диафонии). Явление консонанса проще всего пояснить с помощью струны. Дело в том, что при звучании струн, кроме основного тона, соответствующего их длинам, всегда имеются более высокие и постепенно уменьшающиеся по амплитуде тоны, кратные двум, трем и т. д. основным тонам (их называют обертонами). Причем звучание основного тона с обертонами именуется тембром. Для примера рассмотрим две струны, основные частоты которых 200 Гц и 400 Гц, то есть их отношение составляет октаву. Предположим, что вместе с основными звучат еще пять обертонов. Это значит, что первая струна будет издавать звуки на частотах 200, 400, 600, 800, 1000, 1200 Гц, а вторая – 400, 800, 1200, 1600, 2000, 2400 Гц. Видно, что при их совместном звучании есть три совпадающих тона – 400, 800 и 1200 Гц. Это звучит приятно и согласованно. Предположим, что вторая струна была расстроена и ее основной тон составляет 410 Гц. Это значит, что она будет издавать звуки на частотах 410, 820, 1230, 1640, 2050 и 2460 Гц. При одновременном звучании с первой струной появятся близкие тона 400 и 410 Гц,800 и 820 Гц, 1200 и 1230 Гц. Как это будет звучать? Плохо, и вот почему. Звук есть гармоническое продольное колебание воздуха, и описывается формулой s t =Asin ωt
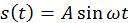
. Следовательно, сумма двух колебаний s 1
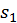
, и s 2
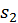
с одной амплитудой будет иметь вид s t = s 1 t s 2 t =Asin ω 1 t Asin ω 2 t=
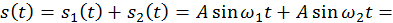
=2Asin ω 1 ω 2 2 tcos ω 1 ω 2 2 t.
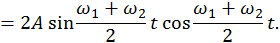
При ω 1 ≈ ω 2
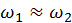
это будет похоже на один звук с частотой ( ω 1 ω 2
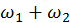
)/2, который будет иметь периодично – с частотой ( ω 1 – ω 2
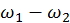
)/2 – изменяющуюся амплитуду. Такие колебания называются биениями, а ( ω 1 – ω 2
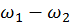
)/2 – частотой биения. Слышится это как своеобразное завывание, которое особенно нестерпимо при частоте биения 33 Гц и исчезает примерно при 130 Гц. Так возникает диссонанс. Древние, конечно, не знали этой теории, но они прекрасно слышали диссонансы и экспериментально искали и находили такие интервалы тонов, которые давали наилучшие консонансы. Диатоническая гамма – первая и простейшая из таких находок.
Μέλος – греч., напев, мелодия. Мед по-гречески звучит примерно также – μέλι.
Диез. У пифагорейцев (Филолая) диезом назывался меньший полутон, так как большой полный тон, то есть разница квинты и кварты (3/2:4/3=9/8), делился на меньший полутон (256/243) и больший полутон, апатомэ, (2187/2048). Причем это разделение было обусловлено тем, что один тон не делится на два равных полутона (невозможно найти рациональное число, квадрат которого давал бы 9/8). Зато оно удобно тем, что диез является интервалом, на который кварта превосходит два тона (4/3:(9/8х9/8)=256/243), а квинта – три тона (3/2:(9/8х9/8х9/8)=256/243). Обычно диез вычитали из тона, а апотомэ прибавляли к нему. Поскольку очевидно, что октава состоит из квинты и кварты: 2/1=3/2х4/3 или кварты, тона и кварты: 2/1–4/3х9/8х4/3 (что соответствовало реальной игре на двух соединенных тетрахордах, настроенных на кварты), то это и позволяло создать дорийскую (мажорную) гамму диатонического наклонения из двух тонов, меньшего полутона, трех тонов и меньшего полутона, начиная с ми первой октавы и далее по нисходящей. Затем, во времена Боэция диез равнялся просто четверти тона (Boet., Inst, mus., I, 21). Впоследствии диезом стали называть повышение звука на полтона. Заметим, что и в этом, и в предыдущем определении Исидор интервалом (spatium) называет соотношение частот, а не отрезок времени. Того же словоупотребления придерживались и многие из древних, как, например, Дионисий Галикарнасский и Архит в трактате «О музыке». Наконец, необходимо коротко рассказать о соотношении пифагорейской октавы и современной. Октава как музыкальный интервал осталась неизменной, изменился лишь принцип построения интервалов внутри нее. Поскольку октава получается при делении струны пополам, то повышение тона ровно в два раза становится как бы само собой очевидным. А вот как поделить это расстояние? Пифагор поделил его на пропорциональные отрезки. В пределах одной октавы такое слушается вполне приемлемо, однако проблемы начинаются при выходе за пределы этого диапазона. Если продолжать откладывать столь же равные отрезки за границей октавы наверх, например, мы придем к следующей октаве гораздо быстрее, ибо если даже посмотреть на струну, видно, что следующая октава получается при делении настоящей пополам, то есть расстояние между основными тонами в два раза меньше. А продолжая откладывать одинаковые отрезки, мы будем сначала попадать между полутонами, а потом с удивлением обнаружим, что уже перешли границу новой октавы, а тонов прошли отнюдь не семь, а меньше. Эта истина дошла до сознания народа где-то веке в XV, наверное, и тогда было предложено практически современное деление, а именно: частота каждого следующего звука (полутона) получается домножением частоты предыдущего на корень 12-й степени из двух, что отличается от пифагорейских значений меньшего полутона и тона в третьем знаке после запятой. Тогда октава по-прежнему получается из тонов, отличающихся по частоте в 2 раза, а промежуточные интервалы получаются более логичными и, что самое главное, более благозвучными. Более того, отсчитав 8 ступеней-нот (12 полутонов) от любого промежуточного тона, мы получим именно октаву, а не неизвестно что. Проблемы возникли только с интервалами терция и секста. Здесь уже дело не в математике, а в восприятии человеческим ухом биений, получающихся при сложении колебаний. Дело в том, что если построить благозвучную большую терцию от, например, ноты до (это получится, в современной нотации, ми), а затем построить благозвучную большую терцию от получившегося тона (в нашем примере: ми – соль-диез), то получившийся тон будет отнюдь не соль-диезом, и не ля, и не соль, а чем-то посередине. Кстати, индусы заметили это очень давно, и в их гамме используются не полутоны, а четверти тона. Посему инструменты настраивали по-разному (это, разумеется, не относится к инструментам типа скрипки, где музыкант может извлечь любой мыслимый интервал, который подчас невозможно записать нотами) пока не был разработан Хорошо Темперированный Клавир, коему И.-С. Бах посвятил два альбома прелюдий и фуг. С той поры музыкальный строй придерживается описанного принципа и нет причин, по которым следовало бы что-либо менять. Что касается конкретной привязки тонов к частотам, то она имеет меньшее значение, чем относительная настройка тонов. Поэтому такая привязка всегда несколько различалась, пока в середине прошлого века не договорились считать ноту ля первой октавы за 440 Гц, что дает для ноты до субконтроктавы (самой нижней) значение около 16 Гц, то есть такое, ниже которого человеческое ухо уже не воспринимает звук как звук. (Мы признательны за этот комментарий Dr. Leopoldus’y, лидеру группы «Llanfair. Р. G.», http://www.llanfair.spb.ru).
Его (тона) рода музыканты разделили на 15 частей, из которых гиперлидийский – новейший и самый высокий, а гиподорийский – самый низкий. Речь о так называемых ладах. Поскольку, как мы сказали, диатоническая октава делится на пять тонов и два меньших полутона (диеза), то возникал вопрос, как распределить эти два полутона между пятью тонами. В древности было три лада, которые отличались тем, что в дорийском (ми-мажорном) ладу полутона шли в конце каждого тетрахорда: ми́ – тон – ре́ – тон – до́ – полутон – си – тон, разделяющий тетрахорды, – ля – тон – соль – тон – фа – полутон – ми. Во фригийском («ре-минорном») ладу полутона занимали среднее положение: тон – полутон – тон – тон, разделяющий тетрахорды, – тон – полутон – тон, и, чтобы сохранить расположение по нотам ступеней лада, весь лад понижался на один тон, что давало ре́-до́-си-ля-соль-фа-ми-ре. В лидийском ладу тетрахорды начинались с полутонов, что давало еще понижение всей октавы на тон: до́-си-ля-соль-фа-ми-ре-до. За всеми тремя наклонениями закрепились эмоциональные клише: говорили о воинственности дорийского, чувственности фригийского и грусти лидийского лада. Понятно, что философы, например Платон и Аристотель и их последователи, очень не любил и два последних. Затем по тому же принципу – порядку чередования тонов и полутонов – было построено семь ладов: гиподорий- ский (ля́-ля), гипофригийский (соль'-соль), гиполидийский (фа́-фа), дорийский (ми́-ми), фригийский (ре́-ре), лидийский (до́-до), гипердорийский (он же миксолидийский, си́-си), где приставки «гипер- /гипо-» означали повышение/понижение звука на квинту, а ступени располагались по восьми нотам звукоряда. Ко временам Боэция и Исидора существовало уже 15 ладов, с шагом в полтона (попеременно диез и апатомэ): гиподорийский, гипоиастийский, гипофригийский, гипоэолийский, гиполидийский, дорийский, иастийский, фригийский, эолийский, лидийский, гипердорийский, гипериастийский, гиперфригийский, гиперэолийский и гиперлидийский. Таким образом, гиперлидийский был выше гиподорического на семь тонов (См. Cass., Inst., И, 5,8). Об особенностях построения ладов для струнных инструментов см. примечание к гл. 22, §5.
Арсис и тесис. О них см. кн. I, гл. 17, §21, и там же гл. 18, §1, и примечания к этим местам.
В завершение теоретической части этой главы надо указать еще на одну сторону античной музыкальной теории, которую Исидор обошел вниманием. Мы уже говорили о диатоническом наклонении, однако их всего было три. Поскольку октава делилась на кварту-тон-кварту, то можно было предложить несколько способов деления самой кварты (4/3). Древнейший способ, восходящий еще к Пифагору или его ближайшим ученикам, был диатоническим: кварта делилась на два тона и один меньший полутон: 9/8х9/8х256/243=4/3, то есть если мы возьмем нижнюю кварту дорийского лада: ля-соль-фа-ми малой октавы. Так поступал Филолай, и это деление заимствует Платон в «Тимее», а за ними – Дидим. Однако уже Архит предлагает еще два наклонения: энгармоническое и хроматическое. Энгармоническое у Ар- хита начиналось с большой терции: 5/4х36/35х28/27=4/3; в нем, как видно, все интервалы суперпартикулярны. Впоследствии это превратилось в удвоенный тон, большую и малую четверти тона, то есть приблизительно: ля-фа-фа-без-четверти-ми. Хроматическое наклонение по Эратосфену состояло из полуторатонового интервала (9/8х256/243–32/27), большого и малого полутонов: 32/27х2187/2048х256/ 243=4/3, что дает приблизительно ля-фа-диез-фа-бекар-ми. Так настраивался нижний тетрахорд. Аналогично в интервале ми́-соль, настраивался верхний тетрахорд; и разница между ними по-прежнему оставалась равной одному тону (9/8). Хроматическое наклонение оказалось довольно популярным, так как позволяло тонко выражать эмоции поэтического текста. Зато энгармоническое наклонение, видимо занесенное с востока, не прижилось, так как считалось слишком мрачным и суровым (правда, у него были и влиятельные сторонники, например трагик Еврипид), и впоследствии кочевало только по музыкальным теориям.
Орга́н был изобретен Ктесибием из Александрии (рубеж II-I вв.) и назывался первоначально, надо полагать, «механическим орудием» (μηχανικὴ ο=᾿ ργανον). Он состоял из 20–50 трубок типа больших свирелей, глиняных или бронзовых, и приводился в движение воздухом из воздушной камеры, который подавался в трубки под напором воды (затем от воды отказались). Достоинствами нового инструмента были большая сила звука, широкий диапазон (до 4 октав) и легкое, клавишное, управление. Поэтому он быстро вошел во всеобщее употребление – в театрах, в цирках и даже в домашнем музицировании. Конструкция органа описана римским последователем Ктесибия – Витрувием (I в.).
Труба. Хотя латинское tuba, соответствующее греческой салпинге, принято переводить словом «труба», надо сказать, что этот инструмент в римской армии был в действительности больше похож на современную тубу. Этот инструмент к римлянам попал через этрусков, которые создали усовершенствованный вид трубы – загнутый кверху сигнальные рожок, литуус. В римской армии оба использовались для подачи сигналов: труба – у пехоты, литуус – у конницы. Предшественником трубы являлся корн – бычий рог, срезанный у острия. Однако римскую трубу нельзя считать, в свою очередь, предшественником современных медных духовых инструментов ввиду отсутствия прямой эволюции. Прототипы наших медных духовых появились не раньше XI века н. э.
Флейта. Этот термин отражает общепринятый перевод латинского tibia или греческого «авлос», хотя, как сегодня полагают, голос этого инструмента походил на звук гобоя, а не флейты. Авлос у греков мог быть двойным и применялся не только при похоронах, но в театральной музыке, для сопровождения пляски и гимнастических упражнений. Считалось, что его мягкий и тягучий голос больше, чем голоса других инструментов, волнует человека и пробуждает в нем страстные чувства. Наши археологи подтверждают, что самые ранние инструменты этого типа состояли из полых костей с боковыми звуковыми отверстиями. Вероятно, флейты имели символическое значение, то есть были связаны с представлениями об охоте и о таинствах жизни, смерти и воскрешения.
Ведь у греков голос называется φω̂ς, а издавать – στολία. Исидор путает φω̂ς – свет и φωνή – звук. Испускать – στέλλω, испущенный – στείλασα (так как латинское vox и греческое φωνή – женского рода).
Самбук и пандура. С двумя последними инструментами много неясностей, так как оба считаются струнными: самбук (тригонон) – вид треугольной по форме арфы, а пандура (пандурин) – трехструнный инструмент, разновидность лютни. То, что Исидор описывает под именем пандурина, – это хорошо известный инструмент – сиринга, или флейта Пана, – вид губного органчика.
Ci.: Iubal вм. Tubal (см. тж. Гл 16)
Использование кифары было открыто Аполлоном. Хотя «использование кифары», возможно, и было открыто Аполлоном, но сама кифара (лира) была изобретена Гермесом (Меркурием) после того, как он украл из священного стада Аполлона коров. Причем корпус был сделан из панциря черепахи, а струны – из кишок двух убитых коров. Затем состоялся обмен: Аполлон получил полюбившийся ему инструмент, а Гермес – животных. После всей этой истории Аполлон научился играть на кифаре и делал это лучше, чем кто-либо из богов и людей (Apoll., Bibl., III, 10, 2). Иную версию этой истории см. ниже. Вероятно, предок кифары (лиры) был исторически первым щипковым музыкальным инструментом: древние люди должны были обратить внимание на звон тетивы лука. Этот инструмент состоял из резонатора, пружинных стоек и поперечины; струны равной длины, но разного натяжения крепились одним концом к резонатору, другим – к поперечине. Резонатором служил панцирь черепахи или выдолбленное дерево, обтянутое кожей. Стойки делались из дерева или из рогов. Струны изготавливались из скрученных кишок животных. Музыкальный инструмент этого типа встречался в различных культурах; в случае Эллады предком кифары была черепаховая форминга, инструмент аэдов и рапсодов, упоминающийся у Гомера, а дальним потомком (через лютню) – современная гитара.
Ci.: pectines вм. pectides.
Эти семь струн кифары или семь частей диатонической октавы (вместе с восьмой, из следующей октавы) назывались: нета (ми первой октавы), паранета, трита, парамеса, меса (квинта от неты и кварта от гипаты), лиханос, паргипата, гипата (ми малой октавы). Меса соответствовала нашей ля малой октавы (Stob., I, 21, 7d). Причем считалась (согласно Пиндару), что первая кифара-форминга, изготовленная Гермесом, была тетрахордом, а гептахорд (семиструнник) придумал Терпандр Лесбосский в VII в. К V в. количество струн достигло 14 (15), и эти две октавы, от ля первой октавы до ля большой, назывались «большой совершенной системой», причем для всех струн были свои названия (см. у Боэция). Игра на кифаре и родственных ей инструментах вносила одно существенное дополнение в теорию семи ладов. Поскольку на кифаре фиксировались тона неты и гипаты, то для струнных инструментов октава всегда строилась от ми́ до ми. И если с дорийским (мажорным) диатоническим ладом все было просто: ми́ – ре́ – до – си – ля – соль – фа – ми, то остальные шесть ладов были вынуждены привязываться к этой дорийской октаве, при этом сохраняя то чередование тонов и полутонов, какое характеризовало данный лад. Это давало, например, для фригийского («минорного») лада диатоническую гамму: ми – ре́ – до́ – диез – си – ля – соль – фа – диез – ми, для лидийского: ми́ – ре́ -диез – до́ – диез – си – ля – соль – диез – фа – диез – ми, для миксолидийского: ми '- ре́ -до – си – бемоль – ля – соль – фа – ми и т. д. для всех семи. Таким образом, лира и кифара были для древних тем и хороши, что могли настраиваться по-разному, в зависимости от необходимости. Разумеется, допускалась и одновременная игра настроенных по-разному кифар, если это давало консонансы. Например, известна мелодия «для двух кифар с оркестром» в смешанном диатонико-хроматическом наклонении.
Лира – упрощенная кифара, поэтому в историческое время она использовалась непрофессионалами, детьми, чаще всего – для обучения игры на кифаре. Различали два типа лир: хелис и барбит. Первая имела резонатор из панциря черепахи и пружинными стойками из рогов антилопы. Вторая отличалась более длинными изогнутыми стойками. В средние века лира была известна под именем «ротта». Отсутствующий в греческом языке глагол λυρέω находится целиком на совести Исидора, который ошибочно считает, что так по-гречески называется разнообразие голосов. Линдсей от отчаяния предлагает толкование α=πὸ του̂ ληρει̂ν («от болтания вздора»).
Тимпан был инструментом типа бубна с широким ободом, или, точнее, тамбурином без тарелочек. Использовался, в основном, во время разных сомнительных с – моральной точки зрения оргиастических мистерий, например дионисийских. Римляне с их прямолинейным, рациональным мышлением очень не любили эту сторону жизни. О симфонии (бубне) как музыкальном инструменте см. ниже, §14.
Кимвал (литавры) состоял из двух металлических тарелок и применялся в оргиастических культах. Впоследствии этим словом стали называть различные малые ударные инструменты – трещотки, колокольчики и др.
Систр – трещотка, состоявшая из скобы, на которую были нанизаны металлические пластинки. Он являлся непременным атрибутом культа Исиды, весьма популярного в Риме и Греции эллинистического периода. Вполне вероятно, что он и в самом деле был изобретен в Древнем Египте, хотя главным музыкальным инструментом этой культуры была арфа.
О среднем гармоническом см. гл. 8, §3. Гармоническим (музыкальным) оно называлось потому, что не выводило за пределы множества рациональных чисел, которое лежало в основании теоретической музыки древних. Заметим, что предложенный Исидором способ вычисления этого числа, c h
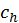
==а(b–a)2/(ab), ошибочен и в предложенном примере совпадает с правильным, c h
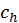
==2ab/(ab), лишь случайно, в силу того, что взято b=2а. Хотя сама формула – «на какую часть оно превосходит, на такую и его превосходят» – верна.
Титул IV. Об астономии. В ряде рукописей этот титул выделяется в самостоятельную, четвертую, книгу «Этимологий», что дает для всего сочинения объем не в 20 книг, а в 21.
Звезды, созвездия и светила. При переводе терминов «astra», «sidus» и «Stella» мы пользуемся указаниями самого Исидора (см. главу 60), то есть «sidus» – это созвездие, «astra» – звезда, а что касается родового понятия «Stella», то мы переводим его как «светило», поскольку Исидор включает в него и планеты, а иногда – Солнце и Луну. Заметим, что наш автор часто уклоняется от упомянутого разделения (см., например, в главе 63). Кроме того, применительно к движению звезд, планет, Солнца и Луны Исидор почти всегда употребляет термин cursus (бег), а не motus (движение), однако мы оба термина обычно переводим как «движение», поскольку в большинстве случаев употребление слова «бег» режет ухо русского читателя, например: «астрономия... касается бегов созвездий» или «неизменные и определенные бега звезд». Обращение светил вокруг себя – вокруг Полярной звезды.
Автор Иосиф утверждает, что Авраам наставил египтян в астрологии – см. Ios., Ant. Iud., 1, 7–8. Иосиф Флавий (37–100 гг. н. э.) – иудейский полководец и писатель-историк, участник Иудейской войны 66–70 гг. н. э., сражавшийся сначала на стороне своего народа, а затем плененный римлянами и принявший их сторону. Автор «Иудейских древностей» в 20 книгах, посвященных истории иудейского народа от сотворения мира до правления Нерона, а также «Иудейской войны» в 7 книгах, описывающей современные ему военные события. Авраама называют переносчиком знаний из Месопотамии в Египет, потому что он был выходцем из «Ура халдейского», бежавшим впоследствии в Египет. Кроме того, Авраама считали сведущим в различных земных и небесных явлениях (см. ссылку на Бероса и Николая Дамаскина в упомянутом месте у Иосифа).
Птолемей, царь александрийский. Здесь ошибочно смешаны Птолемеи, цари эллинистического Египта из династии Лагидов (305–30 гг.), и Клавдий Птолемей (после 83 – после 161 гг. н. э.) – великий греческий астроном, астролог, математик и географ. Его главным сочинением было «Математическое собрание» в 13 книгах (ок. 140 г.), название которого европейскому читателю более известно в своем искаженном арабском переводе – «Альмагест». В нем были собраны и развиты все основные достижения греческой астрономии. Книга I представляет общие методологические установки и краткий очерк геоцентрической системы мира в своем наиболее развитом варианте. Книга II – самая ранняя из дошедших до нас работ по тригонометрии. Книги III-V посвящены движению Солнца и Луны, расстояниям до них, исчислению года и месяца. Книга VI касается движения планет. Книги VII-VIII посвящены неподвижным звездам, даны координаты и величины 1022 звезд. Остальные книги более детально описывают геоцентрическую систему мира, очерченную в первой книге. Вот его основные труды: «Четверокнижье» – очень популярный в средние века астрологический сборник, «Гармоника» в трех книгах – музыкальный трактат, в котором рассматриваются и критикуются все греческие музыкальные теории; «Оптика» в пяти книгах, содержащая в том числе теорию отражения, «Об основаниях» и «Планисферия» посвящены теории проекций, «Руководство по географии» в – восьми книгах – грандиозный математико-географический проект, по которому на карте мира, выполненной в конической проекции, даются около 8000 координат различных географических пунктов.
Астрология же – наука частично природная, частично суеверная. Сегодня мы знаем астрологию как лженауку о будто бы существующей связи между судьбами людей и расположением светил, в особенности во время их рождения. Однако не следует недооценивать прогрессивного ее значения для своего времени. Ведь она устраняла мифический произвол богов, а потом и Бога и их влияние на земные события и судьбы людей, подчиняя мир математически описываемым непреложным законам природы, естественным законам движения светил. Она призывала людей наблюдать и рассчитывать, а не молиться. Это просветительское значение астрологии в древности заметил еще Лукиан Самосатский (см. его трактат «Об астрологии»). Поэтому мы вправе считать, что для великих ученых античности – Гиппарха, Птолемея и других – астрология представляла физическую гипотезу, объяснявшую устройство мира в единстве его земных и небесных законов, во взаимовлиянии неба и земли, также как геометрические астрономические теории служили для описания наблюдаемых явлений. Наш автор, следуя Аврелию Августину, относится к астрологии крайне отрицательно (см. гл. 71, §§37–40). Кроме того, надо отметить, что в классической Греции термины α=στρονομία и α=στρολογία были синонимами и обозначали начала астрономии, а не астрологии. Например, Платон употребляет исключительно термин α=στρονομία, тогда как Аристотель и его последователи – только α=στρολογία. (сочинение Евдема по истории теоретической астрономии называлось «ʼΑστρολογικὴ»). Последним фактом весьма злоупотребляют современные астрологи. Разделение этих понятий началось во II-I вв. в связи с распространением собственно астрологии.
Распределяют двенадцать небесных знаков по отдельным частям тела и души. Такая «астрономическая медицина» была характерна для школы Гиппократа Косского. См. сочинение «О диагностике» Иоанна Актуария (XIV в. н. э.).
Глава 30. О форме мира. Весь пассаж о форме мира, возможно, навеян Verg., Georg., 1,231 –256. Конечно, из приведенного определения трудно сделать вывод о том, как Исидор представлял себе мир. Значительно облегчает дело его популярный учебник «О природе вещей», в особенности главы 9–27. Космос у него состоит из трех частей: неба, Земли и подземного мира. При этом небо со всеми находящимися на нем сферами светил шарообразно, а Земля непостижимым образом плоская (см. здесь гл. 43), круглая, обтекаемая океаном. Античный астрономико-географический термин «земная сфера» (orbis) он понимает как «земная окружность». В данной главе под «миром» имеется в виду именно Земля. Частей земли четыре – восток, юг, запад и север. Такое разделение заимствовано у Вергилия и Лукана. Однако «областей», то есть континентов, только три – северный (Европа), восточный (Азия) и южный (Африка). В центре мира расположен Иерусалим, а главная сторона света, куда обращено лицо мира, – восток, поскольку там располагается земной рай. Представление о том, что Земля плоская, – это, конечно, заметный шаг назад по сравнению с античной географией, и связан он со стремлением совместить античную эллинскую картину мира и библейскую, при превосходстве второй во всех спорных случаях. А поскольку еврейская космология времен великих пророков была не оригинальной, а заимствованной из Вавилона, то мы становимся свидетелями возрождения в VI- VII вв. н. э. вавилонской космологии рубежа II-I тыс. до н. э. Действительно, мы находим у Исидора плоскую землю, как бы плавающую в мировом океане (гл. 47,62) и покрытую полусферой неба (гл. 39,43). Врата запада и востока (гл. 40) – это знакомые вавилонские «Гора восхода» и «Гора заката», закрытые на замок. И т. д., и т. п. Такую же позицию занимал старший современник Исидора, александрийский купец Косма Индикоплов (VI в.) в своей «Христианской топографии», однако в Византийской империи это умопомрачение прошло гораздо быстрее: преп. Иоанн Дамаскин (кон. VII в. н. э.) и свт. Фотий, патриарх Константинопольский (IX в.), считают шарообразность Земли очевидной истиной.
Небо называется α=πὸ του̂ ὁράσθαι. Ср. с платоновской этимологией: «А имя Уран... прекрасно выражает “взгляд вверх” (ὁρω̂σα τὰ α=᾿ νω), который, по словам людей, изучающих небесные явления, сохраняет в чистоте человеческий ум» (Plat., Crat., 396с).
Сфера неба. Это то же самое, что сфера «неподвижных звезд». Аристотель в трактате «О небе» поясняет, что термин «небо» употребляется в трех значениях – 1) вращающаяся сфера «неподвижных звезд»; 2) часть мира, находящаяся между сферой Луны и сферой звезд, то есть Солнечная система, говоря современным языком; 3) все, что находится внутри сферы звезд, то есть Вселенная (Arist., Cael., 1,9). О доказательствах сферичности неба и его вращении см. у Ptol., Aim., I, 3.
Философы же ввели семь небес мира, то есть планет. Упомянутые философы – Евдокс Книдский и его ученик Калипп. Далее в крайне сжатой форме излагается теория гомоцентрических сфер Евдокса (см. также примечание к гл. 67). Семь «планет» – это Луна, Солнце, Венера, Меркурий, Марс, Юпитер и Сатурн, которые имеют форму шара (globi).
Северный полюс, который никогда не заходит,., и южный полюс, который никогда не виден. Сразу ясно, что человек писал, находясь в северном полушарии. В южном полушарии все будет наоборот, это знали греки уже в III в. до н. э., но не знал Исидор, так как считал землю плоской. Борей – северный ветер, Австронот – южный; оба имени использовались в переносном значении для обозначения севера и юга. Первыми же людьми, которые догадались, что вращение небесной (звездной) сферы можно объяснить вращением земного шара вокруг своей оси, были, видимо, пифагорейцы Гикети Экфант(Сю., Acad., 11,39,123; Hippol., Наег., 1,15). Эту идею подхватил Платон (Plat., Tim., 40b), и затем это учение было развито платоником и перипатетиком Гераклидом Понтийским. К такому выводу философы пришли из-за несоответствия скорости обращения сфер и их удаленности. Действительно, расстояния до планет они справедливо поставили в зависимость от периодов их обращений, то есть чем ближе планета к Солнцу (или, как тогда считали, к Земле), тем быстрее она обращалась: например, Луна – за месяц, две нижние планеты – меньше, чем за год, Солнце – за год, а Сатурн – вообще за 30 лет. И вот за Сатурном была сфера звезд, которая делала полный оборот за 24 часа! Логично было заключить, что причина последнего вращения, если исходить из его скорости, должна быть где-то между центром Земли и кругом Луны, то есть как раз на земной поверхности, которую и предположили вращающейся. После этого сфера неба (звезд) стала считаться вообще покоящейся, то есть как раз сферой «неподвижных звезд».
Сфера неба поворачивается... за двадцатичетырехчасовые промежутки времени, за которые Солнце, вращаясь, завершает свой бег над землею и под землею. Тут автор допускает серьезную неточность, поскольку все три промежутка времени – звездные сутки, 24 часа и солнечные сутки – не равны между собой и древние это хорошо знали. Сегодня это можно пояснить следующим образом. Прежде всего, с точки зрения земного наблюдателя Солнце медленно движется относительно звезд в обратном направлении – с запада на восток, то есть по эклиптике, совершая полный круг за год. Значит, звездные сутки, равные времени полного оборота Земли вокруг свой оси относительно «неподвижных» звезд, короче солнечных суток примерно на 4 мин. И если бы мы приняли звездные сутки за 24 часа, то примерно через полгода момент верхней кульминации Солнца (когда оно поднимается над горизонтом выше всего) пришелся бы на 12 часов ночи. Во-вторых, и с солнечными сутками все не просто. На их продолжительность сильно влияет географическая широта, поскольку Солнце проходит в разные времена года разные пути по небу. Поэтому в зависимости от того, как считать солнечные сутки – от восхода до восхода или от заката до заката – будут получаться разные значения для длительности суток. Например, у нас в северном полушарии в средних широтах весной Солнце восходит раньше, чем накануне, поэтому продолжительность времени «ночьдень» весной всегда больше времени «деньследующая ночь» (ведь каждая следующая ночь короче предыдущей): первая сумма больше, а вторая меньше 24 часов. Эту сложность можно было бы обойти, выбрав для точек отсчета начала и конца суток моменты, не зависящие от широты, например, считать от одной верхней кульминации Солнца до другой. Но и такой промежуток времени, который называется истинными солнечными сутками, не равен 24 часам. Дело в том, что Земля движется вокруг Солнца не равномерно по кругу, а по эллипсу, и, кроме того, на ее движение влияет Луна. Следовательно, видимое движение Солнца относительно звезд неравномерно, что заметил еще в V в. Метон Афинский. Поэтому сегодня за 24 часа мы принимаем средние солнечные сутки, причем разница между средним солнечным временем и истинным, называемая уравнением времени, доходит по абсолютной величине примерно до 16,5 минут. Древние римляне в этом случае поступали несколько по-иному: они принимали за 12 часов промежуток времени от истинного восхода до истинного заката и столько же часов считали в ночи. В этом случае солнечные сутки всегда были равны 24 часам, зато сам час не оставался фиксированным временным интервалом: ночные «часы» отличались от дневных, а летние дневные «часы» были гораздо длиннее зимних.
И названа она осью... Поскольку там есть Возок. Ось мира проходит очень близко от Полярной звезды, входящей в созвездие Малой Медведицы, которое иначе называлось Возком, Возом (Plaustrum) . У воза есть оси. См. примечание к гл. 71, §6.
Полюса мира суть окружности, которые движутся по оси мира... И названы они... от шлифования. Такое весьма странное определение объясняется, очевидно, тем, что Исидор представлял себе ось мира стержнем ненулевой толщины, а полюса – кольцеобразными ступицами, через которые она проходит (как ось повозки через ступицы колес). Витрувий, например, сравнивает их с кружочками-держателями оси на токарном станке (Vitr., IX, 1, 2). Этимология фантастическая, так как автор производит «полюс» от глагола polire – «полировать», «шлифовать», «делать гладким», имея в виду, что ось в ступице шлифуется до блеска, тогда как на самом деле слово πόλος греческое и восходит к πέλω – «двигаться». В следующем предложении Северный полюс мира назван правым, так как для Исидора «лицо» мира обращено на восток, следовательно, северное – это правое, а южное – левое.
Третья часть неба – северная, куда Солнце приходит с более длинными днями; четвертая – южная, куда Солнце приходит, когда ночи длиннее дней. Совершенно правильное наблюдение. Например, на экваторе все время от момента весеннего равноденствия до осеннего Солнце будет находиться только в северной половине неба, а от осеннего равноденствия до весеннего – в южной. В средних широтах Солнце бывает и в северной части неба, и в южной, но здесь уже считают, где оно бывает дольше.
Семь полярных звезд. Имеются в виду семь самых крупных звезд Малой Медведицы. Ниже Северный полюс мира назван центром вращения, или вершиной мира, поскольку такое словоупотребление имело место, однако он, конечно, не вращается.
Есть и другие семь параллелей неба. Впервые использовать параллели и меридианы стали Евдокс и, особенно, перипатетик Дикеарх (жил ок. 300 г.), родоначальник математической географии, у которого нулевой меридиан проходил по линии «Днепр-Родос-Нил», а нулевая параллель – по линии «Гибралтар-Родос». Географическая сетка из семи параллелей и семи меридианов была предложена еще Эратосфеном (III в.), и за одним исключением (Месопонт) параллели у него проводились именно через пункты, упоминаемые Исидором: Мероэ (19° с. ш.) – столица древнеэфиопского царства, расположенная у четвертого нильского порога; Сиена, ныне Асуан (24° с. ш.), – самый южный из городов Верхнего Египта, находящийся у первого порога; Κατὰ χώρας досл. «нижние земли», – это Нижний Египет, то есть дельта Нила (30° с. ш.); Родос (36,5° с. ш.) – большой греческий остров у юго-западной части Анатолийского полуострова и главный город этого острова; Геллеспонт, ныне Дарданеллы (40,5° с. ш.), – один из проливов между Эгейским и Черным морями; Месопонт, это дословно «середина Понта» – Черного моря (около 44° с. ш.); Борисфен, то есть устье Борисфена, ныне Днепра (47° с. ш.). Таким образом, ширина каждого пояса получается примерно в 4–5°. Затем, вскоре после изобретения глобуса Кратетом Малосским, разделение меридиана от полюса до экватора на 90° предложил Гиппарх (II в.), и в дальнейшем для картографии строились цилиндрическая (Марин Тирский, нач. II в. н. э.) и коническая (Птолемей, сер. II в. н. э.) проекции земного шара. Подробнее см. Ptol., Aim., И, 6. Параллели Исидора соответствуют пятой, седьмой, девятой, одиннадцатой, тринадцатой, пятнадцатой, семнадцатой птолемеевским параллелям. Греческий термин κλίμα, дословно «наклон», очень многозначен. Первоначально, он, видимо, означал наклон земной оси на разных широтах. Как географический термин со значением «параллель», «широта» впервые употреблен Евдоксом и Дикеархом. Затем так стали называть области, параллельные пояса на земном шаре и господствующие в каждом таком поясе климаты в современном смысле этого слова. Об упомянутом влиянии климата на нравы и здоровье людей см., например, трактат «О воздухе, водах и местностях» (V в.) из гиппократовского корпуса, сочинение Клавдия Галена «О местностях» (И в. н. э.) или «Четверокнижье» Птолемея.
Поясов неба пять. Учение о климатических поясах Земли – это общее место античных писателей, так как попадает в пересечение предметных областей натурфи: лософии, описательной географии (хорографии), математической (координатной) географии, астрономии и медицины. Право первооткрывателей этого учения оспаривают Пифагор (Aristox., frg. 24) и Парменид Элейский (Parm., frg. А 44а Лебедев), что, впрочем, не есть противоречие, ибо сам Парменид учился у пифагорейца Аминия и вряд ли был оригинален при изложении натурфилософских взглядов во второй части своего знаменитого философского эпоса. Компендиум всего учения читатель найдет в «Метеорологике» Аристотеля. Излагаемая ниже теория извлечена из сочинений стоика Посидония (кон. II в.), при этом нарушен порядок кругов: зимний тропический на самом деле шел перед антарктическим. Обитаемыми областями – то, что у эллинов называлось «ойкуменой», – считались только два пояса: от полярных кругов до тропиков, один – в северном, другой – в южном полушарии (см. Arist., Meteor., II, 5; Ptol., Aim., II, 1).
Арктос – доcл. греч. «медведь». Аркты – созвездия Большой и Малой Медведиц. См. гл. 71 §§6–7 и 35.
Зодиак. Греч. ζω̢διακός – «звериный» (подразумевается «круг»), – это 12 со-звездий, лежащих в плоскости эклиптики. Невероятное определение Исидора можно объяснить так, что под Зодиаком он понимал окружность с равномерно расположенными на ней 12 точками – зодиакальными созвездиями. Эта окружность описана около звезды, которая образована из шести линий, пересекающихся в центре и соединяющих оппозиционные знаки (ср., например, его определение таких знаков в гл. 14). Одну из этих линий, вероятно, ту, что рисовалась вертикально, он почему-то выделяет. К созвездиям Зодиака всегда было приковано особое внимание астрономов древности, поскольку в них происходили все наблюдаемые события Солнечной системы: движение Солнца, Луны, планет; вернее сказать, почти только эта часть неба и находилась под наблюдением.
Это есть путь, по которому кружится Солнце, и светит он так, перенимая его сияние. В ошибочности этого утверждения легко убедиться, сравнив положение эклиптики и Млечного Пути – они не совпадают даже приблизительно. То, что Млечный Путь состоит из множества неразличимых невооруженным глазом звезд, первыми открыли Анаксагор и Демокрит, по словам Аристотеля, который подробно исследует вопрос о Млечном Пути (Arist., Meteor., I, 8). Экспериментально это подтвердил только Г. Галилей после изобретения телескопа.
Когда восходит, Солнце одновременно показывается равно на востоке и на западе. Кажется, автор полагает, что Солнце по всей Земле восходит одновременно (так как считает Землю плоской), хотя из этого аргумента нельзя сделать вывода о величине Солнца. Любопытно, что Птолемей доказывал шарообразность Земли как раз неодновременностью восходов и закатов светил (Ptol., Alm., 1,4). Знание о величине Солнца напрямую зависит от знания расстояния до него. О расстояниях в космосе первым заговорил Анаксимандр (Anax., frg. А 19 Лебедев). Что касается вычисления расстояния от Земли до Солнца, то первую научную попытку определить его предпринял Аристарх Самосский в сочинении «О размерах и расстоянии до Солнца и Луны». Он использовал метод триангуляции, выбрав момент, когда диск Луны ровно наполовину освещался Солнцем, то есть центры Земли, Луны и Солнца составляли прямоугольный треугольник. Измеряя угол между направлениями на центр Луны и центр Солнца, можно вычислить расстояние до Солнца в единицах расстояния до Луны (которое Аристарх рассчитал ранее другим методом). Исходя из расстояния до Солнца и его видимого диаметра, он рассчитал величину Солнца. Правда, разница между 90° и упомянутым углом оказалась столь мала, что Аристарх невольно завысил ее в 21 раз: в результате расстояние до Солнца (а значит, и размер Солнца) у него оказалось во столько же раз меньше истинного. Однако ошибки подобного рода неизбежны в пионерских работах, и они бледнеют перед смелостью и принципиальной истинностью мысли этого астронома, который, опираясь на систематические наблюдения, создал удовлетворительную модель Солнечной системы, свободную от теологических представлений, и заложил основы современной космологии. Настоящий диаметр Солнца – ок. 1 391 000 км.
Солнце выше Луны. Исидор не вполне ясно представляет себе природу расстояний в Солнечной системе (даже в ее геоцентрическом варианте): он смешивает понятия «выше», в смысле угловой высоты светила над горизонтом, и «дальше», в смысле космических расстояний между небесными телами. (См. также в гл. 53.) Поэтому мы, переводя, употребляем термины «Земля» или «земля» в зависимости от того, идет ли речь о небесном теле или о «плоской» земле, отождествляемой с плоскостью горизонта.
Величина Луны меньше величины Солнца. Исидор считает, что видимый диаметр Солнца больше лунного, очевидно, потому, что при солнечном затмении из-за диска Луны видна солнечная корона. Видимые угловые диаметры светил изменяются в следующих пределах: Солнца – З1'27» –32'З1», Луны – 29'24, –33'40«. Зная расстояние до Луны и ее видимый диаметр, Аристарх сумел вполне удовлетворительно вычислить ее размеры (см. примечание к гл. 57). Настоящий диаметр Луны – 3476 км.
Философы говорят, что огонь Солнца питается водою. Первым из упомянутых философов был Фалес Милетский, который полагал, что Солнце питается водными испарениями (Thai., frg. A 11, 12а Лебедев). Совмещение несовместимых элементов объясняется тем, что Солнце испаряет, как бы притягивает к себе воду, и, кроме того, роса бывает по утрам, значит, считали древние, ее источает Солнце. Поэтому оно будто бы влажное. Но уже Аристотель, как известно, считает такую позицию «достойной осмеяния» (Arist., Meteor., II, 2: 355а). Среди четырех «элементов» античной натурфилософии – огня, воздуха, воды и земли – огонь и вода считались противоположными. См. также «О природе вещей» нашего автора, гл. 15.
Солнце движется... Сегодня мы видимый годовой путь Солнца по звездной сфере называем эклиптикой. О том, что эклиптика наклонена к плоскости небесного экватора, знали еще в глубокой древности, например, Гесиод, но угол наклона вычислил Энопид Хиосский, причем вполне точно: 24°, что лишь немного отличается от известных сегодня 23°27' Сейчас мы понимаем, что плоскость эклиптики – это плоскость, в которой (с небольшими отклонениями) вращаются планеты нашей Солнечной системы, а угол ее наклона к плоскости небесного экватора объясняется углом наклона земной оси к плоскости эклиптики. Заметим, что Исидор знает о движении Солнца относительно сферы звезд, а также о том, что это движение производит смену времен года. Понять причину зимы и лета он не может, лишь констатирует, что зима – это когда Солнце на юге, а лето – когда на севере.
Овощи и плоды, которые варятся во влаге. Процесс созревания плодов считался процессом их варения в собственном соку под действием солнечного тепла. См. Arist., Meteor., IV, 3.
Когда же оно движется на юг, оно ближе к земле, когда же оно вблизи севера, оно поднимается выше. Здесь, конечно, речь не о расстоянии между Землей и Солнцем в разные времена года, а о том, что зимой Солнце поднимается ниже над горизонтом, а летом – выше. Нижеследующую часть главы Линдсей приводит по Is., De nat. rerum, 17, 3, ссылаясь на некоторые второстепенные рукописи «Этимологий» (codices Leidensis, Karolinus и др.).
Святитель Т. Флавий Климент Александрийский (ок. 150 – ок. 215) – пресвитер и христианский учитель в Александрии, руководитель Катахетической школы (после смерти Пантена ок. 200 г.), глубокий знаток языческой литературы, гностических и христианских учений. Находился под некоторым влиянием гностицизма. Главные его труды – «Строматы» (семь книг богословско-литературной мозаики теоретического характера) и «Педагог» (труд нравственно-воспитательного характера) – являются ценнейшими источниками для истории античной философии, науки и литературы благодаря содержащимся в них цитатам более чем 360 греческих авторов.
Вся последняя часть главы, начиная со слов «Ему, поэтому, Бог установил...», в Поблетской рукописи отсутствует, равно как и чертеж. Однако несколько чертежей сохранились в трактате «О природе вещей», и в данном случае, очевидно, описана знаменитая роза ветров Исидора, восходящая (не непосредственно!) к «Метеорологике» Аристотеля (Arist., Meteor., II, 6). Вся фигура расположена в плоскости горизонта, а перечисленные точки соответствуют следующим ветрам Аристотеля (по часовой стрелке): Δ -эвру, Θ – ноту (юг), Γ – либу, Α – зефиру (запад), Ε – аргесту, Η – борею (север), Ζ – кекию, Β – апелиоту (восток). Направление на юг названо шестым часом дня потому, что день делился на 12 часов, то есть полдень наступал как раз в шесть часов. Азимуты точек восхода и захода Солнца в дни зимнего и летнего солнцестояния названы точками восхода и захода в Рождество Господне и Рождество Иоанна Предтечи, из чего следует, что эти праздники приходились, по нашему календарю, на 21 декабря и 21 июня соответственно. (Современный церковный календарь несколько отошел от этих дат.) Углы ΔΟΘ, ΘΟΓ, ΕΟΗ и ΗΟΖ равны между собой и, конечно, зависят от географической широты: в Севилье они составляют примерно 60°. Все эти чертежи были чрезвычайно популярны в средние века, в частности, роза ветров Исидора, по мнению Ж. Фонтэна, – это уже готовая роза готического собора. По этому поводу см. FontaineJ. Isidore de Séville. Traite de la natura, suivi de l’Espι̂tre en vers du roi Sisebut a%` Isidore. – Bordeaux, 1960. – P. 296, а также стихотворение «Окнороза» P.-M. Рильке.
Некоторые философы говорят, что Луна имеет собственный свет. Это очень древняя точка зрения. Известно, что ее держался Анаксимандр, хотя объяснение Исидора скорее отвечает учению Гераклита о чашеобразных Солнце и Луне. Первым, кто открыл, что Луна светит отраженным светом, считается Анаксагор (но не Анаксимен, как ошибочно указывает Теон Смирнский). Споры на эту тему закончились еще в V в., и непонятно, как они могли попасть в сочинение, написанное 11 веков спустя.
Седьмой же с половиною день лунного месяца и двадцать второй с половиною – в ее окружности средние, а прочие дни – долевые. Автор принимает синодический месяц за 30 суток (на самом деле 29 суток 12 час. 44 мин. 2,78 с и это значение, к слову сказать, еще Гиппарх вычислил с точностью до 1 с), причем в упомянутые дни Луна находится соответственно в первой и последней четвертях, то есть освещена наполовину. В первоначальном римском календаре день первой четверти Луны назывался Нонами, а начало месяца – Календы – старались подогнать под новолуние.
Она движется по косой орбите, а не по прямой, как Солнце. Уже со времен Гиппарха было известно, что Луна движется не в плоскости эклиптики, а в другой плоскости, которая наклонена к эклиптике на 5,1°. Кстати, известно было и то, что Луна перемещается не по круговой орбите, с чем справедливо связывали некоторую не-равномерность ее движения относительно звезд. Объяснение Исидора причины «косого» движения Луны совершенно неверно: если бы она находилась постоянно в плоскости эклиптики, то есть перемещалась относительно звезд по тому же пути, что и Солнце, она все равно не упала бы на Землю.
Луна ближе к Земле, нежели Солнце. Аристарху удалось придумать остроумный способ определения расстояния до Луны (выраженного в радиусах Земли) по средней продолжительности лунного затмения и периода орбитального движения Луны. Это расстояние получилось равным примерно 60 радиусам Земли (по современным подсчетам, около 63,8). Радиус же Земли был вычислен Эратосфеном с точностью до 1%.
Затмения Солнца и Луны. Первым, кто предложил изложенные здесь совершенно правильные причины затмений, был Анаксагор из Клазомен (сер. V в.). См.: Plat., Crat., 409a-b; Aet., II, 29, 6–7.
Созвездия, звезды. Здесь очевидно перепутаны примеры к терминам sidera и astra. То есть созвездия Ориона и Волопаса – это, конечно, «многие светила», а скопления Гиад и Плеяд – это пример образования «больших светил», так как считалось, что большиеи яркие звезды – это скопление множества мелких.
Светила не имеют собственного света. Это, конечно, верно для светил-планет и неверно для светил-звезд. Утверждение, что звезды светят отраженным светом, сравнительно позднее и не характерно для времен расцвета греческой астрономии.
Ci.: multa minora вм. multae maiores. Вероятно, переписчик отнес оба прилагательных к слову claritas (яркость) из предыдущего предложения, но тогда получается трюизм: большую видимую яркость имеют те светила, которые видимы более яркими. Мы предлагаем отнести оба слова к слову intervalla (расстояния), которое фигурирует в названии главы.
Светило обегает свой круг или по долготе, или по широте. Широты и долготы здесь астрономические (эклиптические), то есть широта – расстояние до эклиптики, а долгота – расстояние по эклиптике, начиная с точки весеннего равноденствия.
Для планет «круговое число» определяется здесь как наименьшее общее кратное сидерического (по долготе) и драконического (по широте) периодов, но фактически приводятся цифры НОК для сидерического периода и тропического земного года. Поскольку точно эта задача не решается, то, в зависимости от заданной точности, можно получить сколь угодно большие числа, однако при небольшой точности (96–98%) получаются вполне астрономически значимые отрезки времени: например, в случае с Марсом – это 15–17-летний период между великими противостояниями, а для обеих дальних планет – просто их сидерические периоды. Цифры, приведенные Исидором для нижних планет, можно исправить: число 9 для Венеры приведено ошибочно вместо 8, а для Меркурия лучше подошли бы 13 лет. Числа для Солнца и Луны, вероятнее всего, просто перепутаны. А именно: лунно-солнечный период в 19 лет был вычислен еще Метоном из Афин, так как за это время проходит почти ровно 235 синодических месяцев, то есть Луна в возвращается в свое исходное положение относительно Солнца, Земли и звезд. Период обращения Солнца вокруг Земли в геоцентрической системе отсчета как раз и принимается за один земной тропический год, продолжительность которого со времен Гиппарха принималась за 365,24(6) дней. Для сравнения приведем цифры, которые указывает Птолемей со ссылкой на Гиппарха (на самом деле они принадлежат вавилонянам): Меркурий – 46 лет, Венера – 8 лет, Марс – 79 лет, Юпитер – 71 год, Сатурн – 59 лет, а для Луны – периоды в 18 и 54 года (Ptol., Alm., IX, 3; IV, 2). Кроме того, указаны очень странные имена планет. Венера названа своим архаичным именем (Lucifer), Марс – Вечерней звездой (Vesper), очевидно, просто по ошибке, так как уже давно было известно, что Вечерняя и Утренняя звезды – это одна планета, а Юпитер именуется Фаэтоном. (О названиях планет см. примечание к главе 71, §18–20.)
Солнце... лучей своих мощью путь заграждает вперед и стоянкой их ход замедляет. Откуда Лукан мог взять такое фантастическое объяснение причин попятного движения планет, остается непонятным. О настоящих научных теориях того времени, объясняющих это явление, мы говорим в примечании к следующей главе. Может быть, источником для поэта послужила какая-нибудь расхожая космологическая или астрологическая гипотеза, известная среди поверхностно образованной римской пуб-лики? См. также гл. 67.
Планеты, то есть «блуждающие». Совершенно верная этимология. По-гречески πλανάομαι как раз и значит «блуждать». Планетами называли такие странные звезды, которые бродят по небу туда и сюда, в то время как все прочие порядочные звезды неподвижно стоят на своих местах и вращаются только вместе с небосводом. (Солнце и Луну тоже иногда относили к планетам.) О них знали еще в древнейшие времена, но у эллинов впервые систематически наблюдать за каждой из них по отдельности стали Пифагор и его ученики: это стало, так сказать, «визитной карточкой» их астрономии. Исследовались пути планет, их блеск, различные периоды обращения, другие циклы. Следовательно, именно Пифагор был открывателем Солнечной системы как совокупности астрономических тел, связанной определенными кинематическими законами. Еще V в. греческие астрономы обратили внимание на то, что планеты движутся приблизительно в плоскости эклиптики, т. е. по зодиакальным созвездиям, и что они выписывают сложные петли, меняя прямое движение на попятное. Сегодня мы знаем, что для нижних планет – Меркурия и Венеры – эти петли обусловлены, главным образом, их собственным обращением вокруг Солнца, а для верхних – обращением самой Земли. Однако в древности этого не знали, но понимали, что объяснять такое странное движение надо: это называлось задачей «спасения явлений, представляемых планетами», то есть задачей нахождения комбинации таких равномерных правильных движений, которые объясняли бы данные явления. Сама постановка этой задачи, а также ее первое решение принадлежали Евдоксу Книдскому (IV в.), который предложил так называемую «теорию гомоцентрических сфер». Он предположил, что движение пяти известных планет описывается четырьмя взаимосвязанными и взаимовлияющими хрустальными сферами, имеющими один центр, центр Земли, но вращающимися с разными скоростями и вокруг разных осей. На движение Солнца и Луны отводилось потри сферы, и последняя, 27-я сфера, объясняла движение звезд. Эта теория была усовершенствована Калиппом, учеником Евдокса, а также философом Аристотелем, который ввел так называемые «ретроградные сферы» для компенсаций движений основных несущих. Получившаяся система состояла уже из 55 сфер (см. Arist., Met., XII, 8). Следующий шаг в объяснении сложного движения планет был сделан Аполлонием, предложившим иной способ разложения движения планет на несколько простых равномерных круговых движений: это были хорошо известные эксцентрическая и эпициклическая модели, то есть модели, согласно которым планета двигалась равномерно по окружности (эпициклу), центр которой сам равномерно двигался по другой большой окружности (деференту), центр которой был смещен на некоторое расстояние (эксцентр) от центра мира. Эти модели были использованы Аристархом при построении гелиоцентрической системы мира, а также Гиппархом; но модель мира Аристарха, основывавшаяся на круговых движениях планет вокруг Солнца, имела недостаточную точность и, в основном, критиковалась. Их же взял за основу Птолемей, который усложнил систему тем, что ввел в нее так называемые экванты. То есть он впервые нарушил аксиому движения Платона, так как движение центров эпициклов по деферентам у него происходит не равномерно, а таким образом, что линия, соединяющая планету с некоторой точкой – эквантом, описывает за равные интервалы времени равные углы. Экспериментируя, Птолемей обнаружил, что проще всего поместить эквант в точку, удаленную от центра деферента на то же расстояние, что и Земля. То есть центр деферента делил пополам отрезок, соединяющий эквант с Землей (Ptol., Alm., III, 3; IX, 5–6; XII, 1–2). Так была пройдена половина пути, отделявшая античные кольцевые орбиты от кеплеровских эллипсов. Вся эта система изумительна с математической точки зрения, так как предвосхищала Фурье-спектроскопию, то есть она являлась геометрической интерпретацией разложения сложной функции в тригонометрический ряд Фурье. С помощью такого метода, увеличивая количество эпициклов (у Птолемея их было 40, а ко времени Коперника, точнее, у его ученика Фракасторо – 79), можно было рассчитать положение светил на небе с любой заданной точностью. Однако эта же система совершенно неудовлетворительна с точки зрения физической, так как дает совершенно неправдоподобные расстояния между светилами. Эти неувязки резко расходятся с экспериментальными данными, например, они дают невероятно большие изменения видимого диаметра Луны, чего не мог не заметить Птолемей. Такое несоответствие геометрии и физики породило гипотезу, споры о которой не прекращаются и сегодня. Согласно этой гипотезе, поддерживаемой школой Нейгебауэра, Аполлонию, Гиппарху и Птолемею было математически безразлично, является ли система мира геоцентрической или гелиоцентрической и каковы реальные пространственные движения Солнца и планет. Их теория была принципиально предназначена для вычисления эфемерид (т. е. положения планет на небе) в рамках той точности, которая была накоплена наблюдениями своего времени. Мы считаем возможным отчасти присоединиться к этой позиции по двум причинам. Во-первых, в своих «Планетарных гипотезах» сам Птолемей развивает как раз физическую, точнее гидромеханическую, модель геоцетрического космоса в духе Аристотеля, но с заменой хрустальных сфер на вращающиеся жидкие тела. Во-вторых, представление о нескольких небесных сфер в духе теории Евдокса и гармонии движения этих сфер в духе пифагорейцев бытовало все средние века; у нашего автора оно тоже встречается (см. гл. 32). И с этим совмещалась птолемеевская картина мира из «Альмагеста» (который перевели с арабского), хотя такое совмещение физически невозможно. В птолемеевской геометрии круги планет пересекаются и уже поэтому не могут быть сферами: такие «сферы» просто переломали бы друг друга. Остается предположить, что средневековые ученые, следуя Птолемею, использовали его систему для расчета эфемерид, тогда как реальная физическая картина мира строилась на основе наиболее прогрессивной для своего времени перипатетической физики, которая исходила из теории гомоцентрических сфер. Но, конечно, совершенно невозможно, чтобы Птолемей был «тайным» гелиоцентристом или чтобы он был безразличен к выбору точки центра мира. В «Альмагесте» он убийственно точно критикует гелиоцентрическую систему Аристарха (Ptol., Alm., I, 5–7), а в «Планетарных гипотезах» недвусмысленно высказывается в пользу Земли как мирового центра.
Светило находится в собственном движении и чему-то против обыкновения предшествует. Здесь у Исидора путаница: термином «предшествование» (προήγησις) применительно к планетам в греческой астрономии обозначалось как раз попятное движение светил, так как в последнем случае движение светила происходит в направлении суточного движения небесной сферы (то есть с востока на запад), обгоняя звезды (ср.: Ptol., Alm., XII, 1). Если «предшествование» применяется для обозначения прямого движения планет (с запада на восток), то это таинственное «что-то», что им предшествует, – это какие-нибудь звезды, от движения которых планеты отстают. Вообще про одно светило говорят, что оно предшествует другому, если оно раньше восходит из-за горизонта, то есть попросту расположено западнее. См., например, определение Цицерона: «Венера, когда она предшествует Солнцу, называется Люцифером».
Падающие звезды. Здесь упрощенно излагается перипатетическая метеорология. Она основывалась, во-первых, на космологическом представлении, что воздушная земная атмосфера простирается до орбиты Луны, а за Луной мир состоит из эфира, «пятого элемента», который был изобретен Аристотелем. Во-вторых, метеорологические, то есть атмосферные, или подлунные, явления объяснялись теорией двух испарений. То есть философ предположил, что под действием солнечного тепла из воды выделяется возносящееся вверх влажное испарение (водяной пар), а из земли – сухое (огненная пневма). Последнее испарение поднимается выше первого и занимает «естественное место» вблизи лунной орбиты, то есть вблизи эфира, частично смешиваясь с его нижними слоями. Эта пневма, собственно, и есть огонь, а те языки пламени, которые мы в быту называем огнем, – это как бы вскипевшая пневма. Соответственно, взаимными влияниями и движениями верхних слоев воздуха, пневмы и эфира Аристотель объясняет такие явления, как метеоры (метеорные потоки, болиды), северные сияния и даже кометы (Arist., Meteor., I, 4–5).
Аркт (Медведица), Септентрион (Трион), Возок (Колесница) – это названия созвездий Большой и Малой Медведиц или только Большой. Медведицей оно названо в честь Каллисто (Гелики), дочери Ликаона, нимфы из окружения Артемиды, которая стала возлюбленной Зевса, была превращена в медведицу и убита Артемидой. После этого Зевс перенес ее на небо и сделал созвездием Большой Медведицы. Малая Медведица – это ее сын, Аркад, не пожелавший расстаться с матерью, или одна из подруг-нимф, также превращенная в медведицу (Apoll., Bibl., III, 8, 2; Ovid., Fast., II, 153–192; III, 108). В Древней Месопотамии это созвездие называлось Мар-гид-да («грузовая повозка»). Удивительно, но во многих культурах мира, в том числе и не связанных между собою, – у вавилонян, индусов, китайцев, южноамериканских индейцев, балтийских народов – это созвездие издревле носило название, имевшее значение повозки, колесницы или упряжного животного. Большая Медведица содержит, по античным подсчетам, 27 звезд, видимых невооруженным глазом, то есть до 6-й звездной величины включительно (здесь и далее количество звезд в созвездиях указывается по Ptol., Alm., VII-VIII).
Медвежий страж (Волопас). Считалось, что он был поставлен Герой, чтобы преследовать ненавистную ей Медведицу-Каллисто и на небе. Однако были разные версии того, кем мог быть этот человек при жизни. Большинство полагало, что это Икарий, который впервые ввел в Афинах употребление вина и был убит людьми, посчитавшими себя отравленными (Apoll., Bibl., III, 14, 7). Другая легенда связана с Триптолемом, сыном Келея. Третью приводит наш автор, см. §35. Созвездие содержит 22 звезды, видимых невооруженным глазом.
Арктур – четвертая по яркости звезда нашего неба. Видимая звездная величина –0,04m. В науке Арктур – звезда вполне заслуженная, так как это первая звезда, которую удалось наблюдать днем (М. де Вилльфранш, 1636 г. н. э.), и у которой удалось определить движение в пространстве (Э. Галлей, 1717 г. н. э.). Этимология Исидора, скорее всего, ошибочна: Арктур – это ʼA=ρκτου ου=̂ρος, «медвежий страж, надзиратель».
Орион. Тут наш автор стыдливо умалчивает о настоящей этимологии имени этого беотийского героя, так как оно происходит oт ου=̂ρον, мочи. По преданию, он был рожден из воловьей шкуры, в которую помочились три бога (Ovid., Fast., V, 531–544: 11 мая; Apoll., Bibl., I, 4, 5). Он был великаном и замечательным охотником, но имел очень много несчастий из-за женщин, от них же и погиб. Гомер утверждает, что и после смерти Орион остался охотником. В Древнем Вавилоне созвездие называлось Сиба- зи-анна («верный пастух небес»). Греки насчитывали в нем 38 звезд.
Гиады. Хорошо заметное невооруженным глазом звездное скопление, образующее «рога» Тельца. В телескоп видны около 100 звезд, расположенных недалеко от звезды Альдебаран. Восходят они по календарю времен Овидия 2 мая. Гиады были дочерьми Атланта и, по одной из версий, были перенесены на небо из-за своего благочестия: они умерли от горя, оплакивая своего рано погибшего брата (Ovid., Fast., V, 164–182: 2 мая; Apoll., Bibl., III, 4,3).
Плеяды. Прекрасно видимое невооруженным глазом рассеянное звездное скопление в созвездии Тельца. Видны 6–9 самых ярких звезд, но всего их около 120 (диаметр скопления – 50 световых лет). Они были также дочерьми Атланта, но по какой причине они оказались на небе, не вполне известно. Возможно, в награду за труды, ведь они разносили богам амброзию. Их восход Овидий относит к 14 мая, заход – к середине ноября (Ovid., Fast., V, 599–602; III, 105; Apoll., Bibl., III, 10, 1).
Она была названа Сириусом, потому что ее знали лучше других звезд. На самом деле, по-гречески σείριος – жгучий, палящий. Сириус (α Большого Пса) – самая яркая звезда нашего неба, не считая Солнца. Он имеет блеск –1,58т и удален от нас всего на 2,67 пк. В Египте он восходил во время летнего солнцестояния и знаменовал начало разлива Нила, а его подъем совпадал со временем наибольшей летней жары, откуда и название – «палящий». В науке эта звезда прославилась тем, что оказалась двойной: в 1862 г. н. э. по расчетам математика Бесселя был открыт белый карлик, названный Сириусом В. Кроме того, в «Четверокнижьи» и «Альмагесте» Птолемей отмечал, что Сириус временами имеет красный цвет наподобие Марса. Сегодня предполагают, что это были вспышки Сириуса В, находящегося в критической фазе свой эволюции.
Кометы. О них в древности было мало что известно: их считали то аномальными планетами, то атмосферными явлениями. Суеверные люди полагали, что они приносят бедствия.
Среди прочих звезд несет больше света. Это совершенно справедливо. Венера является самым ярким светилом нашего неба после Солнца и Луны – ее блеск колеблется в пределах от –3,7m до –4,2m (звездной величины). Вообще Светоносцем или Утренней звездой называли Венеру в период утренней видимости.
Они распространяют свои лучи в виде гривы. Речь идет об эффекте дифракции лучей света, исходящих от некоего источника, в хрусталике человеческого глаза. Благодаря этому эффекту звезды имеют вид не светящихся точек, а как бы «звездочек» () или, в терминологии Исидора, гривы (iuba). Поэтому в латинском языке iubar – это блеск, сияние, но не всякое, а именно такое, «гривастое». Этот эффект довольно заметен для такого яркого светила, как Венера.
Геспер, сын титанида Атланта (или его брат) и Эос. Жил, как и его дочери, Гес- периды, на далеком Западе. См. Diod. Sic., III, 60; IV, 27.
Открытие того, что Утренняя и Вечерняя звезды – это одна и та же планета (Венера), приписывают Пифагору. Римлянам это было известно уже во времена Катулла (LXII, 34 sqq.) и Цицерона (Cic., Nat. deor., II, 20, 53).
Имена планет приводятся, очевидно, по Цицерону (Cic., Nat. deor., II, 20, 51– 53), за исключением Марса, греческое имя которого оратор правильно пишет как Πυρόεις. Цицерон, в свою очередь, заимствует их у Аристотеля (Arist., De mund., 392а23–31). В VI-V вв. планеты у эллинов имели различные наименования и не относились к почитаемым божествам греческой мифологии, то есть их считали не более и не менее божественными, чем, скажем, ночь, день, ветер или зарю. Приведенные имена, видимо, были самыми распространенными, и их перевод таков: «светящий», «сияющий», «огненный», «вечерний», «сверкающий», – подразумевается α=στήρ, звезда, которая в греческом языке мужского рода. Заметно, что только два имени были осмыслены, остальные – просто синонимы. Впервые мысль, что планеты суть боги, высказал Платон в «Тимее», связав это представление с заимствованным у ранних пифагорейцев представлением о равномерном круговом движении планет. Для этого он заимствовал названия планет у вавилонян, сделав греческую кальку имен их богов (по словам его ученика Филиппа Опунтского, когда Платон был уже в преклонном возрасте, его посетил некий халдей). Так и появились современные названия планет, в греческом, конечно, варианте их произношения: Гермес, Афродита, Арес, Зевс и Кронос, что соответствовало вавилонским богам Набу, Инанне-Иштар, Нергалу, Мардуку и Нинурте. (Напомним, что Уран был открыт только в 1781 г. н. э. В. Гершелем, Нептун – в 1846 г. н. э. И. Галле по вычислениям У. Леверье, а Плутон – в 1930 г. н. э. американской обсерваторией им. Ловелла.) Впервые эти имена встречаются в платоновском «Тимее» (Plat., Tim., 38d) и в «Послезаконии» Филиппа Опунтского (986е-987а), а приобрели известность они из-за популярного аристотелевского трактата «О мире», где философ приводит и старые, и новые названия. Цицерон выбирает оттуда только старые, а новые приводит в латинском «переводе»: Меркурий, Венера, Марс, Юпитер, Сатурн. Кроме того, в эллинистическое время, в период всеобщего увлечения разной египетско-вавилонской мистикой, планеты получили еще и сакральные имена, которые мы здесь не приводим именно ввиду их сакральности.
Этот выпад направлен, главным образом, против Овидия, по «Фастам» которого (с некоторыми отступлениями и дополнениями) составлена эта глава.
Средняя линия мира – небесный экватор. Исидор начинает перечисление созвездий Зодиака, начиная с точки пересечения эклиптики и небесного экватора, то есть с весеннего равноденствия. Из-за прецессии земной оси даты нахождения Солнца в созвездиях Зодиака в древности существенно отличались от современных. Это выглядит как медленное смещение точки, например, весеннего равноденствия назад по эклиптике. При этом полный круг совершается за 25729 лет. Так, во времена Платона и Аристотеля это точка находилась в созвездии Овна, на рубеже эр она перешла границу Овна и Рыб и сегодня находится в Рыбах, а после 2600 года н. э. перейдет в созвездие Водолея. Поскольку Овидий жил на рубеже эр, то он был совершенно прав, говоря, что Солнце вступает в созвездие Овна около дня весеннего равноденствия. Зато не прав был Исидор, когда утверждал то же самое. Для этого было достаточно оторваться на время от переписывания старых рукописей и просто взглянуть на небо. Современные астрологи прекрасно осведомлены об этом явлении (прецессии), открытом еще Гиппархом, поэтому в их терминологии «вступление Солнца в знак Зодиака» и «вступление в созвездие Зодиака» – понятия разные и отличающиеся почти на целый знак.
Овен. Этимология названия этого созвездия указана Исидором по неизвестному источнику и с ошибкой. Среди богов египтян бараньи рога имел не Амон, а Хнум; баран же был священным животным Амона в Фивах, а не самим этим богом. Общепринятая же античная версия состояла в том, что на небо был вознесен златорунный баран Гермеса, который увез Фрикса, сына Афаманта, в Колхиду (Ovid., Fast., III, 851 – 876: 23 марта; Apoll., Bibl., I, 9, 1). По-шумерски оно называлось Лу-хун-га («наемный работник»). Греки включали в него 13 звезд.
Телец – это Критский бык. См. Ovid., Fast., IV, 717–720апреля; V, 604–620; Apoll., Bibl., III, 1, 1. У вавилонян – Гу-анна («бык небес»). Состоит из 32 звезд, видимых невооруженным глазом.
Близнецы – это братья Диоскуры, Кастор и Полидевк, сыновья Леды от Тиндарея и Зевса. Поэтому первый был человеком, а второй – богом. После гибели Кастора Полидевк проклял свое бессмертие, и по решению Зевса оба были помещены на небо с тем, чтобы один день проводить на небе, а другой – на земле (Ovid., Fast., V, 693–720: 20 мая; Hom., II., XI, 300 sqq; Apoll., Bibl., III, 11, 2). И они на самом деле возвращаются с небес в том электростатическом явлении, которое мы сегодня называем коронным разрядом. Его хорошо знают моряки, так как в сильную бурю и грозу огни Диоскуров зажигаются на концах корабельных мачт и рей, неся спасение терпящим бедствие людям. Шумерское название – Маш-таб-ба («великие близнецы»). 18 звезд.
Рак. См. Ovid., Fast., VI, 727–728: 19 июня; Apoll., Bibl., II, 5, 2. По преданию, рак впился клешнями в ногу Геракла, когда тот боролся с многоголовой Гидрой. Когда рак был убит, ненавидевшая Геракла Гера отблагодарила это создание тем, что поместила его на небе. Вавилоняне называли его Аль-лул («краб» или «рак»). Всего насчитывалось 9 звезд.
Лев. Считалось, что это тот самый Немейский лев, сын Ортра, которого победил Геракл, совершив первый подвиг из двенадцати (Hes., Theog., 326 sqq.; Apoll., Bibl., II, 5, 1). Однако еще в Шумере это созвездие было известно под именем Ур-гу-ла («лев» или «большая собака»). Состоит из 27 звезд. Этесийские ветры – северные сухие ветры, постоянно дующие летом (с июля по сентябрь) в районе Средиземного моря.
Дева. В Древнем Вавилоне это созвездие называлось Абсин («колос»). Поэтому и в Элладе его изображали в виде девы с пучком колосьев в руке и связывали с богиней плодородия – Деметрой или ее дочерью, Персефоной (Корой). В созвездии насчитывали 26 звезд. Каникулярные дни (каникулы) – это самая знойная пора года – с конца июля до середины октября, – названная так от видного только в это время созвездия Большого Пса (Canis) и его главной звезды – Сириуса (Canicula). В переносном смысле каникулы – это просто невыносимая жара. Разумеется, это было время свободное от занятий в римских школах, которые в то время располагались почти что под открытым небом.
Весы. У этого созвездия была сложная судьба. В Вавилоне оно как раз и называлось Рин («весы»), а в Древней Греции его не считали отдельным созвездием, а относили к Скорпиону в качестве клешней последнего. Но в римское время, в период повального увлечения восточной астрологией, его «восстановили в правах» под вавилонским названием, связав с весами Дики (Фемиды), богини правосудия. В древности к Весам (Клешням) относили 8 звезд. Осеннее равноденствие в начале нашей эры действительно приходилось на созвездие Весов.
Скорпион – это то самое животное, которое нанесло смертельный укус Ориону. По всеобщему мнению, это было заказное убийство, но установить заказчика следствию, как водится, не удалось. Поговаривали, что это была Артемида или Гея. Кто и зачем вознес его на небо, непонятно. По-шумерски назывался также Гиртаб («скорпион»). Включал в себя 21 звезду.
Стрелец. Древнейшее название – Па-Билсаг («конный лучник»). Греки считали, что это кентавр Фол, один из немногих приличных кентавров, который был другом Геракла, но случайно погиб от руки этого героя, когда защищал его от озверевших соплеменников (Apoll., Bibl., II, 5, 4). Целится из лука он как раз в Скорпиона, охраняя от этой твари остальных небожителей. В этом созвездии насчитывалась 31 звезда.
Козерог. Древние шумерские имена Сухур («коза») или Мас («рыба»). Эллины полагали, что в этом виде на небо был помещен бог Пан, а вид этот он получил при следующих трагикомических обстоятельствах. Во время битвы богов с титанами Пан, спасаясь от чудовища Тифона, попытался превратиться в козла, но, поскольку он прыгнул в Нил до того, как превращение было закончено, половина, которая осталась над водой, трансформировалась в козла, а другая половина, под водой, стала рыбьим хвостом. Оказавшись на небе, объединил 28 звезд. Коза, кормилица Зевса – Амалфея (Hom., II., XXI, 194; Apoll., Bibl., I, 1, 5).
Ci. (Линдсей): capream вм. caprem.
Водолей. Греки не могли вполне точно установить, кто был вознесен на небо под этим именем. Чаще всего считали, что это юноша Ганимед, сын царя Троя, ставший любовником Зевса и виночерпием богов (Hom., II., V, 265; XX, 232; Apoll., Bibl., III, 12, 2). Но вспоминали также и Девкалиона, который пережил Великий Потоп (Schol. Hom., II., I, 126; Apoll., Bibl., I, 7, 2). У шумеров – Гула («великан»). По подсчетам эллинов в это созвездие входило 42 звезды.
Рыбы. Считалось, что в этом созвездии был увековечен образ тех двух рыб из реки Евфрат, которые спасли Афродиту и Эрота от Тифона. В Древнем Вавилоне этому созвездию соответствовали три разных: Кун-меш («хвост»), Сим-мах («великая ласточка»), Анну-ни-тум («владычица небес»), но употреблялся и термин Рикис- нунни («лента рыб»), которых насчитывали три. У греков затем их стало две, связанных лентой (всего 34 звезды), а Исидору, как видно, достаточно и одной.
Орел и Лебедь. Оба созвездия связаны с любовными похождениями Зевса на земле. В виде орла он похитил юного пастуха Ганимеда, сына троянского царя Троя (Hom., II., V, 265; XX, 232; Apoll., Bibl., III, 12, 2). А в образе лебедя он сошелся с Ледой, женой спартанского царя Тиндарея (Apoll., Bibl., III, 10, 7). (Подругой версии, это Кикн, царь лигуров, безутешно оплакивавший гибель своего друга Фаэтона, сына Гелиоса.) Созвездие Орла еще у вавилонян именовалось Те («птица»), а Лебедя – Уд-ка-дух-а. Согласно Птолемею, созвездие Орла состояло из 9 звезд, а Лебедя (Птицы) – из 17.
Персей, сын Зевса и Данаи, и Андромеда, дочь эфиопского царя Кефея, – персонажи известного древнегреческого мифа, все основные учасники которого попали на небо: герой-спаситель, спасенная царевна, ее родители (Цефей и Кассиопея) и даже убитое героем чудовище (Кит) (Apoll., Bibl., II, 4, 3). В Древнем Междуречье созвездие Персея именовалось Шуги («старик»), а Андромеды – Лулим («олень»). В первом эллины насчитывали 26 звезд, во втором – 23.
Возничий. По-шумерски Гам («сабля»). Греки же полагали, что это человек, но не знали точно, какой. По одной из версий, это афинский царь Эрихтоний, сын Гефеста, который первым впряг коней в колесницу, первым стал пахать землю плугом, а также учредил праздник Панафиней. Исидор говорит об уподоблении Солнцу, поскольку до Эрихтония колесница была только у бога Гелиоса (Apoll., Bibl., III, 14,6–7). По другой версии, это Миртил возничий элидского царя Эномая, предавший и погубивший этого царя и сам убитый Пелопом (Apoll., Bibl., Ер., 2,6–8). Говорили также, что Возничий – это мчащийся по небу Фаэтон, сын Гелиоса, или даже бог морей Посейдон на своей колеснице. Всего 14 звезд, видимых невооруженным глазом.
Лира. У вавилонян – Уз («коза»). 10 видимых звезд. Миф о лире и Гермесе см. в гл. 22, §2 (и примечание к нему) и §8.
Центравр. Созвездие названо в честь кентавра Хирона, который был самым мудрым и благородным в этом крайне разнузданном племени. Он был рожден бес-смертным, счастливо избежал участи своего народа, был воспитателем героев Актеона, Асклепия, Ахилла, Ясона, но был обречен на вечные мучения после того, как его случайно ранил Геракл. Титанид Прометей предложил себя в обмен и обрел бессмертие, а Хирон скончался и был вознесен на небо (см. Apoll., Bibl., 1,2,4; II, 5,11; III, 13). Правда, поскольку на небе оказалось сразу два кентавра, Хирон и Фол, то люди не всегда знали, который из них Центавр, а который – Стрелец, и часто их путали. У шумеров это созвездие носило описательное название Эн-те-на (Маш-лум) («созвездие холодов (в виде свиньи)»). Насчитывало 37 звезд.
«Ученые христианской религии», которые считали астрологию разновидностью черной магии и порождением Сатаны, – это Ипполит (кон. II – нач. III в. н. э.), Тертуллиан (кон. II – нач. III в. н. э.), Евсевий Кесарийский (вт. пол. III в.), свт. Григорий Нисский (IV в.), бл. Аврелий Августин (кон. IV в. – нач. V в.) и большинство прочих. Борьба с астрологией во времена христианской патристики шла на волне борьбы с гностическими ересями. См. знаменитые «Семь аргументов против астрологии» Августина в книге «Творения Блаженного Августина, епископа Иппонийского.» – Ч. 3. – К., 1907, а также у Св. Василия Великого (Р. G., XXIX, col. 9С). Исидор здесь приводит второй довод Августина. Что касается Платона и Аристотеля, то с их космологией учение о гадании судеб по звездам, действительно, не совместимо. В целом, отрицательное отношение к «халдейским предсказаниям» было характерно для Греции до времен эллинизма (см.: Cic., De div., II, 42, где против астрологии прямо выступает Евдокс, или Gell., XIV, 1).