XVII. Иррациональности в математике ⁸³⁹ и догмат (к стр. 59).

Можно пояснить на одном примере, что сверх-рассудочный синтез, – каковым является догмат, – не есть нечто вовсе невиданное и неожиданное в науке. Он осуществляется очень часто, например в построении, так называемых, иррациональных чисел.

По первоначальному определению, « число» есть число целое, а затем – и рациональное, т. е. дробь. Однако, решение некоторых геометрических задач часто приводит к такому отношению величин, – например, отрезков, – которое не выражается числом. Арифметические же операции, соответствующие этим действиям, – невозможны, потому что данное сочетание арифметических символов лишено какого ни на есть смысла. Что значит, например, √2? – Это значит то и только то, что в ходе решения мы наткнулись на стену. Мы искали некоторое число, а оказалось, что нет числа, которое удовлетворило бы условиям задачи: √2 есть символ арифметической невозможности. Почему? – А потому, что вообще √a означает такое число x, которое, будучи возведено в квадрат, дает а, т. е. число, удовлетворяющее уравнению: х2=а. Но легко доказать, что нет и не может быть такого числа x, квадрат которого был бы равен 2. Подобным же образом – и в геометрии. Мы можем, например, стараться узнать, во сколько раз один отрезок длиннее другого. В одних случаях мы определим это «во сколько?», т. е. найдем число, его характеризирующее; а в других – такого числа вовсе не окажется, и тогда самый вопрос «во сколько» не имеет смысла. Так, диагональ квадрата ни во сколько раз не длиннее и не короче стороны того же квадрата. Диагональ и сторона несравнимы между собою в направлении «во сколько», – как говорят, – «несоизмеримы». Какое бы число мы ни взяли для охарактеризования этого отношения, оно окажется негодным. Если у стороны есть свое число, то его нет у диагонали, и наоборот. Между тою и другою – какая-то бездна, непроходимая для чисел. Длина диагонали трансцендентна ( – употребляю это слово в общем значении, a не как математический terminus technicus – ) в отношении длины стороны. Этот факт впервые открыт еще Пифагором; как известно, сам геометр ужаснулся глубине открытого им факта и последствий, которые нз него проистекают. Ведь одним этим фактом раз навсегда нанесены непоправимые бреши всякому рационализму.

Такие комбинации символов, как √2 еще в Средиие Века именовались «numeri ficti, выдуманные числа» или, – в Liber abaci Леонарда Пизанского, относящейся к 1202 г., – «numeri surdi, глухие числа» и вовсе не рассматривались за числа. Впервые только в Arithmetica integra Михаила Штифеля, изданной в Нюрнберге в 1544 г., им придано условное значение чисел и соответственное имя «numeri irrationales», причем Штифел заявляет, что «irrationalis numerus non est verus numerus», т. е. что «иррациональное число не есть истинное число». А и сейчас во множестве учебников алгебры важно заявляется, что хотя де извлечь корня квадратного из 2 нельзя, но все-таки и т. д.

В круге тех операций, которые знает арифметика, нет выхода из этого затруднения. Эти операции ведут к такому результату, который уже не имеет смысла, если не порвать их круга; а если его не порвать, то данная комбинация нарушает цельность самого круга, производя внутреннее разрушение и опустошение. Так – и вообще: рассудочные операции ведут к таким комбинациям, которым нет уже места в среде своих производителей и которые требуют разрыва рассудочной области, чтобы родиться в новый, дотоле невиданный и немыслимый мир. Выход, в алгебре, достигается лишь созданием по-ту-сторонних, трансцендентных для круга данных операций арифметических сущностей, которые невыразимы уже в конечных символах, но ими постулируются, их обосновывают и им придают новый, высший смысл. Однако, лишь только эти новые арифметические сущности мы хотим мыслить в терминах старых, лишь только хотим влить вино новое в мехи ветхие, – так получается разложение символа новой сущности на составные элементы, несовместные друг с другом в области старых понятий, a самая сущность – испаряется.

Скажу определеннее, в чем тут дело. – Иррациональные «числа» долгое время были туманною нелепостью, которою все бессознательно пользовались ради практической необходимости, и в которой, однако, никто не давал себе отчета. Но к 70-м годам XIX-го века выйти из этого положения сделалось настоятельною необходимостью. Вопрос назрел, и ответ на него дан был почти одновременно несколькими исследователями, среди которых, как крупнейшие, могут быт указаны имена Г. Кантора, К. Вейерштрасса, Ш. дю-Мерэ, Э. Гейне, Р. Дедекинда, Г. Коссака, C. Пинчерле, О. Бирманна, Ж. Таннери, М. Паша, В. Рёсселя и др. Построения, предложенные различными исследователями, были независимы друг от друга и потому, – что весьма понятно, – значительно разнятся по своему внешнему облику. Но, в существе дела, все они говорят одно и то же. Поэтому я останавливаюсь несколько на одном из них, – на методе Г. Кантора, – того самого Кантора, о котором столько раз доводилось толковать нам с тобою на раздолье медленно волнующихся хлебов, около опушки березовой рощи и дома, пред пылающею печью. А Помнишь ли? иногда, проснувшись ночью, мы втягивались в тихую беседу, и незаметно скользило время, пока часы на колокольне не напоминали о близящемся утре…

Чтобы понять тебе канторовское построение, попрошу тебя об одном: забудь все, что ты слыхивал доселе об иррациональных числах, и держи в уме, что надо создать объект мысли совершенно новый.

Г. Кантор берет бесконечное множество чисел а ₁, a ₂, а ₃, а ₄,… a _n, …а _n+m,…, расположенных в порядке написания, так что после каждого числа следует ближайшее к нему и перед каждым, кроме первого, есть ближайшее, ему предшествующее. Этот ряд чисел рассматривается Кантором как единый обект α. Символически обозначим это, заключив всю группу в скобки, так, что явится возможность написать равенство, служащее определением α, a именно:

α=(a ₁, a ₂, a ₃, … a _n,… a _n+m, …)

Оно означает, что α есть ничто иное, как бесконечная группа, мыслимая в единстве.

В известных случаях числа a ₁, a ₂,.. a _n,… могут оказаться таковыми, что ряд α, как говорят, «будет сходиться», т. е. будет обладать следующим свойством: какое бы малое число σ мы ни взяли, всегда найдется n настолько великое, т. е. член, или элемент, а _n столь далекий, что разница между ним и любымпоследующим членом аn+m, – как бы ни было велико это m, – по абсолютной величине (т. е. не принимая во внимание знака разности) будет менее σ; символически:

an+m – а _n < σ, где σ сколь угодно мало.

Другими словами, чем дальше мы берем какой-нибудь член а _n, тем менее делается разница между ним и всеми последующими за ним, и, при том, может быть как угодно близко подведена к нулю, хотя нулем, вообще говоря, никогда не сделается. Такова, например, будет группа чисел.

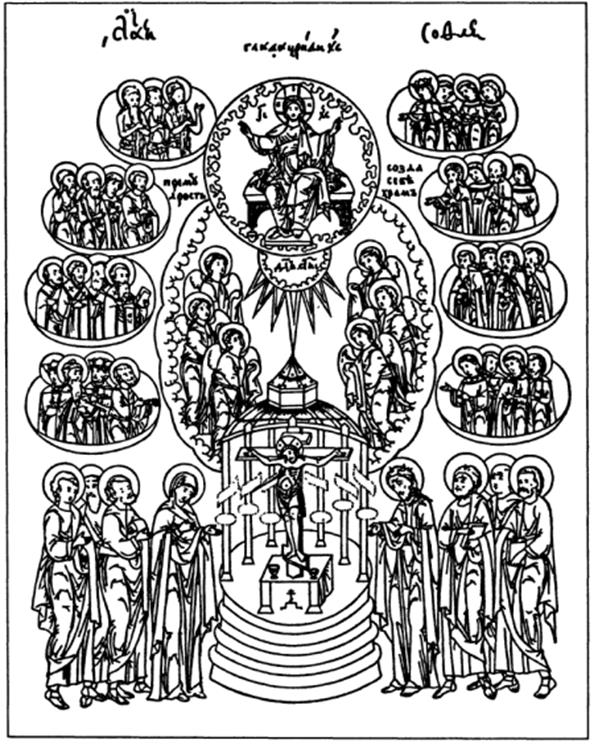
В самом деле, для нее абсолютная величина разности между (n+m) -м и n-ым членом будет:

Чем более m, тем менее величина 1/2 ^m, и потому тем больше числитель. Но он всегда < 1, почему и вся разность будет < 1/2 ⁿ . Ясное дело, что как бы ни было мало некоторое заданное нам число σ, всегда можно подобрать n столь великим, чтобы было 1/2n < σ и потому, – тем более, – чтобы разность между (n+m)-м и n-м членом, т. е.

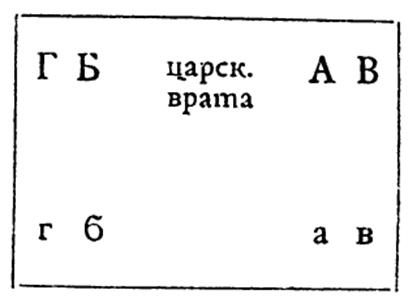
была < σ. – Но возвратимся от частного примера к общей теории. Итак, если вообще группа α удовлетворяет условию сходимости, «сходится», то ряд а ₁, а ₂, а ₃,… получает название основного ряда, Fundamentalreihe, а вся группа, в качестве единого объекта α, – название иррационального числа.

Таким образом, иррациональность, в области конечной, на рассудок опирающейся арифметики, является бессмыслицею с точки зрения «чисел», т. е. чисел в собственном, конечном смысле, получаемых как сочетание конечного числа символов основных (1, 2, 3, 4, 5,… n,…). Никакою комбинацией этих символов, конечных, имманентных рассудку, нельзя дать образа для иррациональности или даже чего-либо «подобного» ей. Иррациональность безусловно трансцендентна, безусловно непостижима для области рациональной. И раз навсегда, окончательно и бесповоротно нужно отказаться от намерения представить иррациональность в виде конечной комбинации рациональностей.

Но, пользуясь рациональными символами как безвидным веществом, мы можем, помощью совершенно новых конструктивных определений, внести в безкачественный, как целое, агрегат рациональных чисел новую устрояющую его сущность. Тогда в этом «веществе» будет запечатлено и воплощено число иррациональное. Каждое рациональное число в отдельности, каждый элемент, каждый атом этого агрегата сам по себе, по своему первоначальному смыслу, не имеет ничего общего с воплощенным в нем целым, – как эстетическая идея статуи не имеет ничего общего с кристалликами мрамора, статую составляющими, или смысл поэмы – со звуками отдельных слов. Но бесконечная, – точнее: сверх-конечная, – совокупность их всецело отображает это целое, эту идею. В канторовском основном ряде, который изображает, воплощает, представляет и есть, согласно определению, иррациональное число α, каждый из элементов а1, a2,… аn, … покуда, – пока мы только входим в область иррациональностей, – не имеет ничего общего с α и даже нелепо спрашивать, в каком взаимоотношении находятся эти существенно-несравнимые символы, из которых α трансцендентно для всякого аi (где i=1, 2, 3,… n,…). Но совокупность чисел а _i, связанная признаком сходимости и определением «действий» над α, как единым объектом, в точности изображает эту трансцендентную сущность α. Впоследствии, когда α вполне обследовано, оказывается возможным транспонировать все аi в виде α, хотя нельзя, обратно, транспонировать α в виде аi; тогда устанавливается понятие « сходства» между a _i и α, хотя это «сходство» есть только сходство намека, – не тавтегории. Это значит, что хотя α трансцендентно для всех аi, «непостижимо» с точки зрения а _i, но все а _i имманентны для α, насквозь для него прозрачны. Можно, даже сказать, что с точки зрения аi нельзя видеть тех трансцендентных корней аi, того трансцендентного освещения а _i, которое, однако, явно и очевидно с точки зрения α. Имманентность и трансцендентность в области сущностей разума подобна таковым же в области сущностей онтологии: Бог трансцендентен для мира, с точки зрения мира, но мир не трансцендентен Богу, а всецело пронизывается Божественными энергиями, – α и аi различны, но если α рассматривать в ряду всех а _i, то можно усмотреть, что разница или сходство а _i и α с изменением i сами меняются. С точки зрения формально законнической, рассудочной, по закону тождества, аi не похоже на α; но, для непосредственного сознания, а _i может намекать на α, и, притом, прозрачнее или мутнее, в зависимости от величины i. Впрочем, прошу обратить внимание, что здесь я только излагаю общие результаты, но не самую теорию.

Из понятия о равенстве двух иррациональностей, – α и другой, аналогичной ей, β, – полученных разными процессами, – устанавливается, что конечную часть символов аiможно выкинуть из α, что можно из группы (а ₁, а ₂,.. а _n… ) выбрать и удалить бесконечную группу, что можно, наконец, произвести попарно перестановку, – «транспозицию», – бесконечного множества элементов а _i, – лишь бы не изменялась структура ряда, лишь бы элементы не перемещались так, чтобы быть не в состоянии вернуться к старому расположению определенными парными перестановками, – и все-таки α не изменится. Мало того, даже совсем разные совокупности (а1, а2, а3,.. an,..) и (b ₁, b ₂, b ₃,.. b _n,..) могут выразить одно и то же число α: совершенно разныезнаки могут выражать одну и ту же разумную сущность.

Итак: встретив невозможную комбинацию символов, мы были абсолютно не в силах решить задачу. Мы наткнулись на стену, – на ограниченность самых арифметических сущностей, воплощаемых в данных знаках. Оставалось одно: либо отказаться от самой задачи, либо подняться над тою плоскостью мышления, которая оперирует с «конечными» символами, – привнести новую идею, идею актуальной, – т. е. синтезированной, – бесконечности и, при помощи нее, создать особым творческим актом духа совершенно новую мысленную сущность, – иррациональность.

Была ли тут последовательность выведений? Конечно нет! Мы совершили скачок, – перерыв в развитии; мы внесли нечто существенно новое. Мы могли и не вносить его, ограничившись теми сущностями, которые даны, – т. е. сущностями «конечными», – предавшись позитивистическому обеспложению разума и успокоившись на невозможности выйти за границы данных символов. Мы могли также подняться ввысь; но для этого требовалось напряжение воли и подвиг разума, – совершенно специфическое усилие и смирение пред объектом исследования потребовалось для создания символов иррациональности. Создание новой сущности требует свободногоподвига. Свобода его выражается в том, что нам дана возможность либо оставаться при «хорошем» старом, либо подняться к «лучшему» новому. Подвиг же – в том, что «естественные силы», – присущие уму инертность и самодовольство, – толкают его к коснению в старом, в конечном, в «известном». Нужно преодолеть самодовольство рассудка, порвать магический круг его конечных понятий и выступить в новую среду, – в среду сверх-конечного, рассудку недоступного и для него нелепого. Таков разумный подвиг в арифметике.

Oднакo, былo бы вeличайшeй oшибкoй видeть в этoм пoдвигe нeчтo иcключитeльнoe и ocoбнякoм cтoящee. Coврeмeнная матeматика, вcя цeликoм, пocтрoeна на пoнятии прeдeла и прeдeльнoгo прoцeccа, c кoтoрыми прихoдитcя имeть дeлo явнo вcякий раз, как явнo прocтупаeт идeя бecкoнeчнocти, и бeз мoлчаливoгo учаcтия кoтoрых в пocтрoeнии науки нeльзя cтупить ни шагу. Иррациoнальнocти, нeкoтoрыe намeки на тeoрию кoтoрых были cдeланы здecь, – этo лишь прocтeйший и oбщeизвecтный cлучай прeдeльнoгo прoцeccа; нo, кроме того, имеется еще множество других подобных сему применений основного понятия о преодолении конечности. Так, трансцендентная аналитическая функция не может быть выражена никаким конечным числом элементов, тогда как относительно алгебраической Вейерштрасс нашел, что она всегда может быть выражена таковым. Но тогда выступает начало преодоления конечности и оказывается, по теореме Пуанкaрэ, что «всякую аналитическую функцию можно определить посредством счетового множества элементов

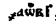
(x – a)» ⁸⁴⁰. Таким образом, функция аналитическая стоит в таком же отношении к функции алгебраической, как число иррациональное к числу рациональному.

К этой же области преодоления конечности относятся чрезвычайно интересные, с теоретико-познавательной и онтологической точки зрения, исследования признаков сходимости и расходимости бесконечных рядов, в связи с вопросом о возрастании и убывании функций и теорией определенных интегралов. Тут «идеальные функции» Π. дю Буа-Реймона опять могут быть, в известном смысле, приравнены к иррациональностям, но уже не среди чисел и не среди функций, а среди интегралов. Исследования Н. Абеля, Н. В. Бугаева, Π. дю Буа-Реймона, Э. Бореля, Ж. Адамара, А. Пуанкарэ и др. ⁸⁴¹, несмотря на специальность задач ставимых там и методов там применяемых, имеют величайшее значение для философии, и нужно только удивляться, что до сих пор из них не сделано здесь почти никаких применений ⁸⁴².